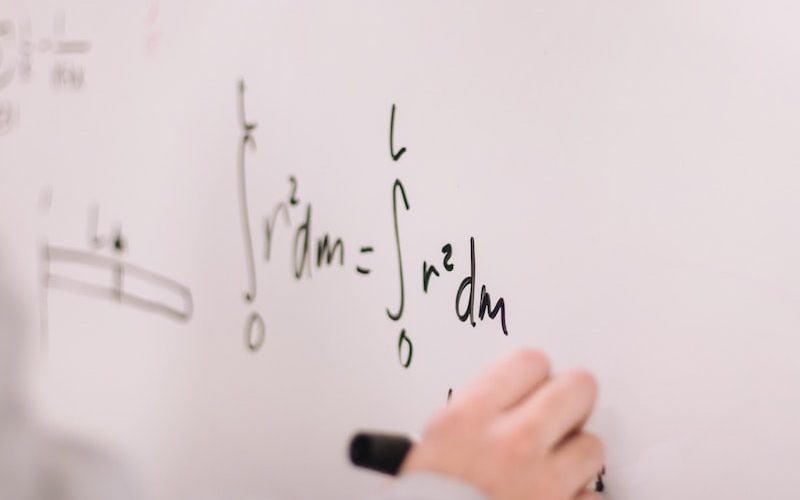Fourier teoremi, matematiksel analizin önemli bir kavramıdır ve bir fonksiyonu frekans bileşenlerine ayırma yöntemidir. Bu teorem, Jean-Baptiste Joseph Fourier tarafından 19. yüzyılda geliştirilmiştir ve genellikle harmonik analiz olarak da adlandırılır.
Fourier teoremi, herhangi bir süreklilikteki periyodik fonksiyonun, sinyal veya dalga formundaki bir verinin, sinüs ve kosinüs dalgalarının toplamı olarak ifade edilebileceğini belirtir. Yani, karmaşık bir dalga formunu daha basit bileşenlere ayrıştırarak anlamamızı sağlar.
Bu teorem, birçok farklı alanda uygulanır. Örneğin, elektrik mühendisliğinde sinyal işlemede, ses ve görüntü işlemede, iletişim sistemlerinde ve fiziksel sistemlerin analizinde kullanılır. Fourier analizi, bir sinyalin frekans bileşenlerini belirlemek için çok etkili bir araçtır ve bu nedenle geniş bir uygulama alanına sahiptir.
Fourier teoremi, matematiksel hesaplamalarda da büyük öneme sahiptir. Bir fonksiyonun Fourier dönüşümü, orijinal fonksiyonun frekans bileşenlerini gösteren bir frekans spektrumu elde etmemizi sağlar. Bu, sinyal işleme, görüntü işleme ve veri sıkıştırma gibi birçok alanda kullanılan bir tekniktir.
Fourier teoremi, doğrusal sistemlerin analizi için temel bir araç olarak kabul edilir. Karmaşık bir sinyali sinüs ve kosinüs bileşenlerine ayırarak, sistemin tepki özelliklerini daha iyi anlayabiliriz. Bu da mühendislik problemlerinin analiz ve çözümünde büyük kolaylık sağlar.
Fourier teoremi, harmonik analizin temel bir parçasıdır ve geniş bir uygulama alanına sahiptir. Fonksiyonları frekans bileşenlerine ayırarak, karmaşık sistemleri anlamamızı ve analiz etmemizi sağlar. Bu teorem, matematiksel hesaplamaların yanı sıra mühendislik, fizik, iletişim ve bilgi işlem gibi birçok disiplinde önemli bir rol oynar.
Müzikten tıbbi teşhislere: Fourier teoremi ve harmonik analizin günlük hayattaki etkileri
Günlük hayatımızın birçok alanında matematiksel prensipler ve fenomenler bulunur. Bu bağlamda, müzikten tıbbi teşhislere kadar geniş bir yelpazede yer alan Fourier teoremi ve harmonik analiz, hayatımızı derinden etkileyen önemli araçlardır.
Fourier teoremi, 19. yüzyıl Fransız matematikçisi Joseph Fourier tarafından geliştirilen bir kavramdır. Temel olarak, bir sinyalin frekans bileşenlerine ayrıştırılmasını sağlar. Müzikte, herhangi bir enstrüman veya ses kaynağından çıkan ses dalgalanmalarının farklı frekanslara ayrıştırılması, müziği duymamızı ve anlamamızı sağlar. Bu nedenle, Fourier teoremi, stüdyo kayıtlarından canlı performanslara kadar müzik endüstrisinde önemli bir rol oynar.
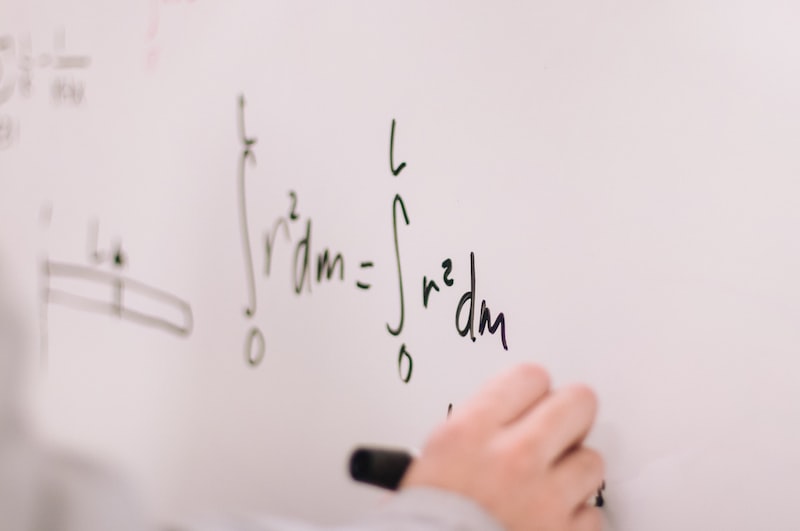
Harmonik analiz ise Fourier teoreminin bir devamı niteliğindedir. Bir sinyalin içerdiği harmonik bileşenleri tanımlamak ve analiz etmek için kullanılır. Özellikle müzik alanında, harmonik analizin kullanımı oldukça yaygındır. Bir şarkıyı dinlerken, farklı enstrümanların ve seslerin bir araya gelerek harmonik bir yapı oluşturduğunu fark edebiliriz. Harmonik analiz, bu bileşenleri belirlememizi ve müziğin duygusal etkisini anlamamızı sağlar.
Ancak Fourier teoremi ve harmonik analiz sadece müzikle sınırlı değildir. Tıp alanında da önemli uygulamaları vardır. Elektrokardiyografi (EKG) gibi tıbbi teşhis yöntemlerinde kullanılan sinyaller, Fourier teoremi sayesinde analiz edilir. EKG sinyali, kalbin elektriksel aktivitesini temsil eder ve bu bilgilerin doğru bir şekilde yorumlanabilmesi için Fourier analizi gereklidir. Bu analiz yöntemi, kalp hastalıklarının teşhisi ve tedavisi için kritik bir rol oynar.
Fourier teoremi ve harmonik analiz, müzikten tıbbi teşhislere kadar geniş bir alanda hayatımızı etkileyen güçlü matematiksel araçlardır. Müzikteki seslerin ayrıştırılması ve anlaşılması, müzik endüstrisinde kaliteyi artırırken, tıpta ise hastaların yaşam kalitesini iyileştirir. Fourier teoremi ve harmonik analizin günlük hayattaki etkileri, matematiğin pratik uygulamalarının bize nasıl büyük faydalar sağlayabileceğini göstermektedir.
Seslerin gizemli dünyası: Fourier analiziyle müziğin sırlarını çözmek
Müzik, insanlık tarihinin en etkileyici ve evrensel sanat formlarından biridir. Ancak, müziğin ardındaki gizemli dünya, genellikle gözden kaçırılır. İşte burada Fourier analizi devreye giriyor ve müziği daha derinden anlamamızı sağlıyor.
Fourier analizi, matematiksel bir yöntemdir ve karmaşık ses dalgalarını daha basit bileşenlere ayırma yeteneğine sahiptir. Bu sayede, müziğin içerdiği farklı frekanslar ve sesler hakkında bilgi edinmek mümkün olur. Örneğin, bir enstrümanın belirli bir nota veya akorunun frekanslarına nasıl tepki verdiğini inceleyebiliriz. Böylece, müziğin tonalitesini ve karakteristik özelliklerini daha iyi anlayabiliriz.
Fourier analizinin temel prensibi, herhangi bir karmaşık ses dalgasının, farklı frekanslardan oluşan basit sinüzoidal (düzlemsel) dalgaların toplamı olduğudur. Bu sinüzoidal bileşenlerin amplitüdleri ve fazları, sesin nasıl duyulduğunu ve algılandığını belirler. Fourier analizini uygulayarak, bir parçadaki bu bileşenleri ayırabilir ve her bir bileşenin müziğe olan katkısını anlayabiliriz.
Bu analiz, müzik üretimi ve kaydı için önemli bir araçtır. Ses mühendisleri, müzik prodüktörleri ve besteciler, Fourier analiziyle seslerin frekans spektrumlarını inceleyerek, enstrümanların ve vokallerin karışımını optimize edebilir, harmonik etkileşimleri kontrol edebilir ve istenen ses kalitesini elde edebilirler. Ayrıca, bu analiz, müzikteki bozulmaları tespit etmek ve düzeltmek için kullanılır.
Fourier analizi aynı zamanda diğer alanlarda da büyük öneme sahiptir. Örneğin, konuşma sinyallerinin işlenmesinde veya görüntü işleme tekniklerinde kullanılabilir. Karmaşık veri setlerini analiz etmek, gürültüyü azaltmak veya belirli desenleri tanımak gibi pek çok uygulaması vardır.
Fourier analizi, müziğin gizemli dünyasına bir pencere açar. Bu analiz yöntemi sayesinde müziğin altında yatan frekans bileşenlerini anlamak ve çözmek mümkün olur. Bu da müziğin nasıl oluşturulduğunu, duyulduğunu ve algılandığını daha iyi kavramamızı sağlar. Fourier analizi, müzik alanında çalışan profesyonellerin ve müzikseverlerin araştırmalarını ve deneyimlerini zenginleştiren güçlü bir araçtır.
Matematiksel bir sihir: Fourier dönüşümüyle görüntülerin saklı mesajları
Görüntüler, hayatımızın ayrılmaz bir parçası haline geldi. Sanat eserlerinden günlük fotoğraflara kadar her yerde görüntülerle karşılaşıyoruz. Ancak birçok kişi, bu görsellerin altında yatan derin anlamları ve saklı mesajları anlama konusunda farkındalığa sahip değil. İşte burada Fourier dönüşümü devreye giriyor.
Fourier dönüşümü, matematiksel bir işlem olarak bilinir ve sinyalleri frekans bileşenlerine ayırma yeteneğiyle ünlüdür. Ancak bu dönüşüm, görsel verileri analiz etmek ve gizli bilgileri ortaya çıkarmak için de kullanılabilir. Görüntülerin Fourier dönüşümü, piksellerin parlaklık düzeylerini frekans bileşenlerine dönüştürerek görüntü üzerindeki desenleri belirginleştirir.
Bu matematiksel sihir, görüntülerin saklı mesajlarını keşfetme fırsatı sunar. Bir örnek vermek gerekirse, bir resmin Fourier dönüşümünü uyguladığınızda, belirli bir frekansa sahip olan bölümlerin vurgulandığını görebilirsiniz. Bu vurgu, resimdeki gizli mesajları ifşa etme potansiyeline sahiptir.
Fourier dönüşümü aynı zamanda dijital görüntülerin sıkıştırılması ve işlenmesi için de kullanılır. JPEG formatında sıkıştırılmış bir fotoğrafı açtığınızda, Fourier dönüşümünün uygulanmış olduğunu göreceksiniz. Bu sayede, yüksek frekans bileşenlerinin azaltılmasıyla dosya boyutu küçültülürken, görsel kalite korunur.
Matematiksel bir sihir olarak adlandırılan Fourier dönüşümü, görüntülerin üzerinde saklı kalmış detayları ortaya çıkaran bir araçtır. Bu dönüşüm sayesinde, sanat eserlerindeki semboller, şifreli mesajlar veya belleklerdeki anılar gibi saklı bilgiler keşfedilebilir. Görüntülerin sadece yüzeyine değil, derinliklerine de inerek matematiğin büyülü dünyasını keşfetmek mümkün hale gelir.
Unutmayın, her bir pikselin arkasında bir hikaye vardır ve bu hikayeleri anlamak için Fourier dönüşümü gibi matematiksel araçlardan yararlanabiliriz. Görsel verilerin saklı mesajlarla dolu olduğunu unutmamalı ve matematiksel sihirle bu mesajları keşfetmeye başlamalıyız.
Dijital çağın temel taşı: Fourier teoremi ve veri sıkıştırma teknolojileri
Dijital çağın hızla ilerlemesiyle birlikte veri sıkıştırma teknolojileri giderek daha önemli hale gelmektedir. Bu teknolojiler, bilgiyi daha az yer kaplayan formata dönüştürerek depolama ve iletişim alanlarında büyük avantajlar sağlamaktadır. Fourier teoremi ise bu veri sıkıştırma sürecinin temel taşlarından biridir.
Fourier teoremi, matematiksel bir kavram olmasına rağmen dijital dünyada büyük bir etkiye sahip olmuştur. İlk olarak Jean-Baptiste Joseph Fourier tarafından 19. yüzyılda geliştirilen bu teorem, herhangi bir periyodik sinyali farklı frekans bileşenlerine ayırma yeteneğine sahiptir. Bu sayede, bir sinyalin karmaşık yapısı analiz edilip, daha az sayıda bileşeni kullanarak temsil edilebilir.
Veri sıkıştırma teknikleri, Fourier teoremini kullanarak veri örüntülerini yakalayabilir ve gereksiz detayları ortadan kaldırabilir. Örneğin, bir görüntüyü sıkıştırmak için Fourier dönüşümü kullanılabilir ve görüntünün frekans bileşenlerine dayanan daha az sayıda piksel kullanarak orijinal görüntüyü yeniden oluşturmak mümkündür. Bu yöntem sayesinde, aynı kalitede bir görüntüyü daha az miktarda veriyle depolamak veya iletmek mümkün hale gelir.
Fourier teoremi ve veri sıkıştırma teknolojileri, dijital çağın temel taşları olarak kabul edilebilir. İnternetin yaygınlaşmasıyla birlikte büyük veri akışlarına dayalı uygulamaların artması, bu teknolojilerin önemini daha da artırmaktadır. Veri sıkıştırma, dosyaların daha hızlı indirilmesini sağlarken, depolama alanı ve bant genişliği kullanımını optimize eder. Bu da internet deneyimini iyileştirir ve maliyetleri düşürür.
Fourier teoremi ve veri sıkıştırma teknolojileri dijital çağın vazgeçilmez unsurlarıdır. Bilgiyi daha etkin bir şekilde işlemek, depolamak ve iletmek için bu teknolojilere olan ihtiyaç her geçen gün artmaktadır. Daha küçük boyutlu verilerin büyük avantajlar sağladığı bu dönemde, Fourier teoremi ve veri sıkıştırma teknolojileri dijital dünyada önemli bir rol oynamaktadır.