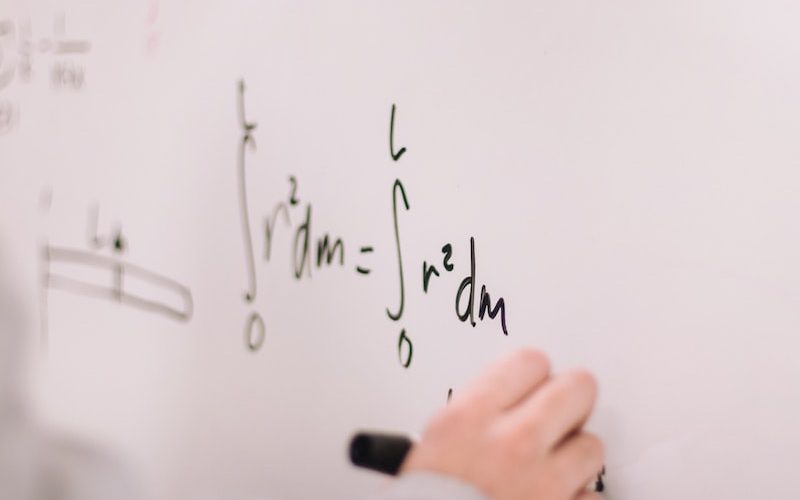Hasse-Arf teoremi, yerel sınıf alan teorisi olarak da bilinen bir matematik teoremidir. Bu teorem, Galois teorisiyle ilgilidir ve sayı teorisi, cebirsel geometri ve cebirsel sayılar teorisi gibi alanlarda önemli bir rol oynar. İlk olarak Helmut Hasse ve Emil Art tarafından formülize edilen bu teorem, cebirsel fonksiyonların köklerinin sayısını belirlemek için kullanılır.
Hasse-Arf teoremi, bir cebirsel fonksiyonun köklerinin sayısı hakkında bilgi sağlar. Özellikle, bir cebirsel fonksiyonun tüm kökleri üzerindeki nokta sayısını hesaplamak için kullanılabilir. Bu teorem, bir cebirsel fonksiyonun köklerinin sayısının, fonksiyonun tanım kümesi üzerinden elde edilen (yerel) sınıf alanının karakteristiği ile ilişkili olduğunu gösterir.
Örneğin, birbirine izomorfik iki eğri düşünelim; bunlar aynı cebirsel fonksiyona karşılık gelen farklı denklemlere sahip olabilir. Hasse-Arf teoremi, bu eğrilerin üzerindeki noktaların sayıları arasındaki farkı açıklamak için kullanılabilir. Teorem, eğer iki eğri farklı birer cebirsel fonksiyona karşılık geliyorsa, üzerlerindeki noktaların sayılarının farklı olacağını söyler.
Bu teorem, Galois teorisiyle sıkı bir şekilde bağlantılıdır. Galois teorisi, köklerin sayısı ve cebirsel denklemlerin çözülebilirlikleri gibi konuları inceler. Hasse-Arf teoremi, bu alanda önemli bir araç olarak kullanılır ve matematikçilerin birçok probleme yaklaşmasına yardımcı olur.
Hasse-Arf teoremi yerel sınıf alan teorisi içerisinde önemli bir yer tutar. Cebirsel fonksiyonların köklerinin sayısını belirlemek için kullanılan bu teorem, sayı teorisi, cebirsel geometri ve cebirsel sayılar teorisi gibi alanlarda büyük bir etkiye sahiptir. Matematikçiler, Hasse-Arf teoremini kullanarak birçok probleme çözüm getirebilir ve matematik dünyasındaki anlayışımızı derinleştirebilir.
Matematikte Gizemli Bir Kavram: Hasse-Arf Teoremi
Matematik, gizemli ve zorlu bir kavramlar dünyasıdır. Birbirinden ilginç teoremler ve keşfedilmeyi bekleyen sırlar barındırır. Bu makalede, matematikteki gizemli bir kavram olan Hasse-Arf Teoremi’ni ele alacağız.
Hasse-Arf Teoremi, cebirsel geometri ve sayı teorisi arasında bağlantılar kurarak, matematikçilerin anlayışını genişleten önemli bir keşiftir. Bu teorem, 20. yüzyılın başlarında Helmut Hasse ve Emil Art tarafından ortaya atılmıştır. İkinci Dünya Savaşı sonrasında Claude Chevalley tarafından daha genel bir şekilde formüle edilmiştir.
Hasse-Arf Teoremi, sayıların nasıl dağıldığına dair ipuçları sağlar. Özellikle, bir polinomun köklerinin modüler aritmetik üzerindeki dağılımını inceler. Bu teorem, sayı teorisindeki birçok problemin çözülmesinde kullanılır.
Teoremin temel fikri, cebirsel bir denklemin köklerinin modüler aritmetik üzerinde nasıl dağıldığını belirlemektir. Bu dağılım, matematikçilere sayıların yapısını anlama ve daha karmaşık sorulara cevap bulma imkanı verir.
Hasse-Arf Teoremi’nin matematiksel ifadesi oldukça karmaşıktır ve derin bir anlayış gerektirir. Ancak, temel düzeyde, bu teorem sayesinde sayıların nasıl dağıldığı hakkında bilgi edinmek mümkündür. Sayı teorisi açısından büyük bir öneme sahip olan Hasse-Arf Teoremi, matematik camiasında halen aktif bir araştırma alanıdır.
matematikteki gizemli kavramlardan biri olan Hasse-Arf Teoremi, cebirsel geometri ve sayı teorisi arasındaki bağlantıları keşfetmemizi sağlar. Bu teorem, sayıların modüler aritmetik üzerindeki dağılımını anlamamıza yardımcı olur ve matematik camiasında halen ilgi gören bir konudur. Hasse-Arf Teoremi, matematik tutkunları için merak uyandıran ve daha derinlemesine keşfedilmeyi bekleyen bir kavramdır.
Yerel Sınıf Alan Teorisi: Hasse-Arf Teoreminin Sırları
Yerel sınıf alan teorisi, cebirsel geometri ve sayılar teorisi gibi disiplinlerde önemli bir rol oynayan, oldukça derinlemesine incelenmesi gereken bir konudur. Bu makalede, Hasse-Arf teoreminin sırlarını keşfedeceğiz.
Hasse-Arf teoremi, cebirsel eşitlikleri çözme sürecindeki bir dizi adımdan oluşur. Bu adımların ardışık olarak takip edilmesiyle, çeşitli matematiksel nesnelerin özellikleri hakkında bilgi elde etmek mümkün hale gelir. Ancak, bu teoremin sırlarını anlamak için, yerel sınıf alan teorisinin temellerini öncelikle anlamamız gerekmektedir.
Yerel sınıf alan teorisi, birbirine bağlı olan lokal alanların incelenmesiyle ilgilenir. Bu alanlar, tam sayılardan oluşan bir halka üzerinde tanımlanan bir yapıya sahiptir. Yerel sınıf alanları, Galois teorisi ile de yakından ilişkilidir ve bu alanda çalışan matematikçiler, cebirsel eşitlikleri çözerken bu teoremle sık sık karşılaşırlar.
Hasse-Arf teoreminin sırları, bu yerel sınıf alanlarının özelliklerini ve ilişkilerini açığa çıkaran matematiksel keşiflerden oluşur. Bu sırları çözmek için, karmaşık matematiksel ifadeleri basitleştirmek ve özgün bir şekilde analiz etmek gerekmektedir. Bununla birlikte, bu teoremi anlamak için sadece matematiksel yetenek yetmez, aynı zamanda yaratıcı bir düşünce sürecine de ihtiyaç duyulur.
Yerel sınıf alan teorisi, sayılar teorisindeki birçok sorunu çözmek için güçlü bir araçtır. Hasse-Arf teoreminin sırlarını çözerek, matematikçiler yeni buluşlar yapabilir ve daha geniş bir anlayışa ulaşabilirler.
yerel sınıf alan teorisi ve Hasse-Arf teoreminin sırları, matematik dünyasında derinlemesine çalışılması gereken önemli konulardır. Bu teoremlerin anlaşılması, matematikçilere sayılar teorisi ve cebirsel geometri gibi alanlarda yeni ufuklar açabilir. Yerel sınıf alan teorisi üzerinde yapılan çalışmalar, matematiksel düşünme becerilerimizi geliştirirken, aynı zamanda bilimsel keşiflerin de kapısını aralar.
Yüzyıllardır Çözülemeyen Bulmaca: Hasse-Arf Teoremi
Matematik dünyasında, tartışmasız bir şekilde çözümü en zor bulmacalardan biri olarak kabul edilen Hasse-Arf teoremi, alansa ilgi duyanlar arasında heyecan ve merak uyandırıyor. Bu teorem, sayılar teorisiyle yakından ilişkili olup, tamamlayıcı bir şekilde çalışan iki önemli matematikçi olan Helmut Hasse ve Emil Artin tarafından formüle edildi.
Hasse-Arf teoremi, cebirsel geometri ile sayılar teorisi arasındaki derin bağlantıyı ortaya koyar. Temelde, bir cebirsel denklemin köklerinin tam sayıları temsil ettiği bir yapı olan sayı cisimlerine odaklanır. Bu teorem, bir sayı cismi üzerindeki bir polinomun tam köklerinin sayı teorisiyle nasıl ilişkilendirilebileceğini açıklar.
Bu teoremin özellikleri ve uygulanabilirlik alanları, matematik camiasında büyük bir ilgi ve şaşkınlık yaratmıştır. Örneğin, Galois teorisi ve cebirsel fonksiyon cisimlerinin sınıflandırılması gibi konularla doğrudan ilişkilidir. Ayrıca, sayı teorisi problemlerinin çözümünde ve kriptografi alanında da önemli bir rol oynar.
Hasse-Arf teoremi, matematiksel karmaşıklığını korurken, aynı zamanda geniş bir uygulama alanına sahip olmasıyla dikkat çeker. Matematikçiler, bu teorem aracılığıyla sayı teorisi problemlerine farklı bir bakış açısı sunarak yeni keşifler yapma fırsatı bulmuşlardır.
yüzyıllardır çözülmesi mümkün olmayan bir bulmaca olan Hasse-Arf teoremi, matematik dünyasında şaşkınlık uyandıran ve hala derinlemesine çalışılması gereken bir konudur. Bu teoremin tam anlamıyla çözülmesi, matematiksel bilginin sınırlarını zorlayacak ve yeni kapıları açacaktır. Hasse-Arf teoremi, matematiksel düşünceye ilgi duyanlar için sonsuz bir keşif alanı sunmaya devam etmektedir.
Matematikçilerin Zihnini Zorlayan Hasse-Arf Teoremi
Matematik dünyası, çeşitli teoremler ve problemlerle doludur. Ancak bazı teoremler, zihinlerimizi gerçekten zorlar ve sınırlarımızı zorlayarak yeni ufuklar açar. İşte matematikçilerin zihnini zorlayanlardan biri: Hasse-Arf Teoremi.
Hasse-Arf Teoremi, cebirsel geometri alanında önemli bir konumda bulunur. Bu teorem, Galois teorisinin bir sonucudur ve tam cisimlerin noktasal yerleşimlerini araştırır. Aslında, bu teorem, bir bölge üzerinde tanımlı bir fonksiyonel denklemi çözmek için kullanılır.
Bu teoremin etkileyiciliği ve zorluğu, karmaşık matematik araçları ve soyut düşünme gerektirmesinden kaynaklanır. Matematikçiler, Hasse-Arf Teoremi’ni çözmek için cebirsel geometri, sayı teorisi ve Galois teorisi gibi birçok disiplini kullanmak zorundadır. Bu teorem, alanında uzmanlaşmış matematikçiler tarafından bile kafa karıştırıcı olarak kabul edilir.
Hasse-Arf Teoremi’nin benzersizliği, onun soyut yapısında yatar. Bu teorem, matematiksel nesnelerin genel özellikleri üzerine derin bir anlayış gerektirir ve kökleri olan polinomlarla ilgilidir. Bununla birlikte, Hasse-Arf Teoremi’nin tam bir kanıtı henüz bulunamamıştır ve bu da matematikçilerin daha fazla çalışma ve çaba sarf etmesini gerektirir.
Bu teoremdeki özgüllük, matematik dünyasında benzersiz bir hazine sunar. Hasse-Arf Teoremi, matematikçilere karmaşık problemleri çözmek için yeni stratejiler sunar ve matematiksel yapıların derinlemesine anlaşılmasına katkıda bulunur.
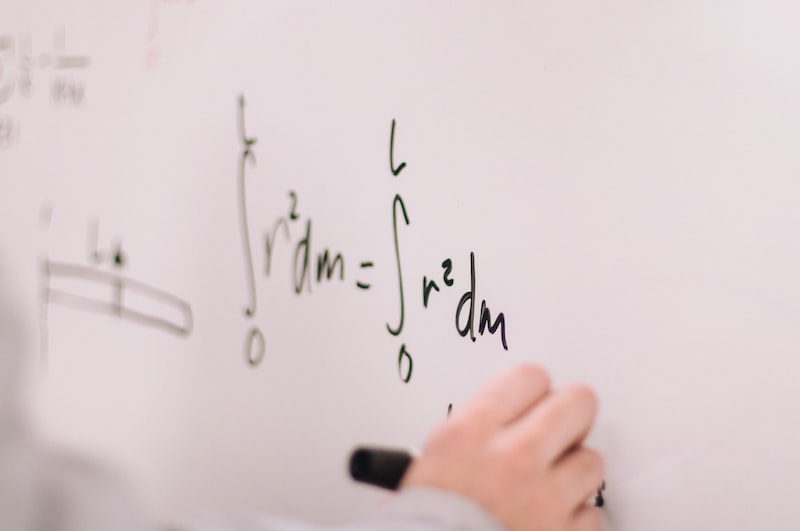
Hasse-Arf Teoremi, matematikçilerin zihnini zorlayan ve onları yeni keşiflere yönlendiren önemli bir araştırma alanıdır. Bu teoremin soyut yapısı ve karmaşıklığı, matematiksel düşünme becerisini geliştirmek için mükemmel bir fırsat sunar. Matematikçiler, Hasse-Arf Teoremi’yle mücadele ederek disiplinler arası bir yaklaşım sergiler ve matematiksel evrenin sınırlarını genişletirler.