türev nedir ispatı- türev nedir ispatı
Daha önce bir doğrunun eğimini hesaplamıştık. Ve o konuda parabol gibi doğru olmayan bir fonksiyonun eğiminin türev yardımıyla bulunacağını söylemiştir. Aslında parabol tarzı yani doğru olmayan bir fonksiyonda genel bir eğim bulamayacağımızdan herhangi bir noktasındaki eğimi bulmamız gerekiyor ve bu noktadaki eğim de o noktaya bir teğet çizilerek bulunuyor. Peki türev ne işe yarıyor?
Böyle doğru olmayan fonksiyonlardan her zaman grafik çizip ne olup ne bitiğini göremiyoruz. Türev bize grafik olmadan cebirsel olarak o noktadaki eğimi bulmaya olanak sağlıyor. Peki bu cebirsel ifadeyi nasıl kuruyoruz?
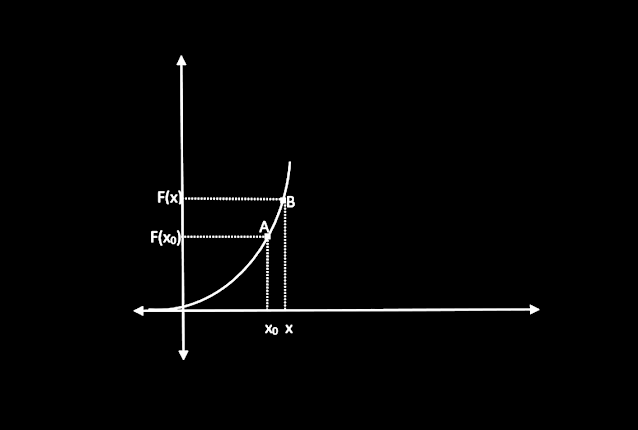
İlk olarak doğrusal olmayan herhangi bir eğri alalım.
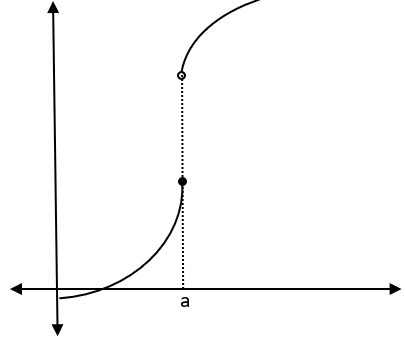
- Bir noktaya teğet çizmemiz için öncelikle o noktanın tanım kümesinde yer alması gerekiyor. Olmayan bir noktaya teğet çizemeyiz.
Yukarıdaki şekilde a noktasına nasıl teğet çizebiliriz? demek ki fonksiyonun a noktasında tanımlı olması yetmiyor. Aynı zamanda sürekli de olması gerekiyor.
3.
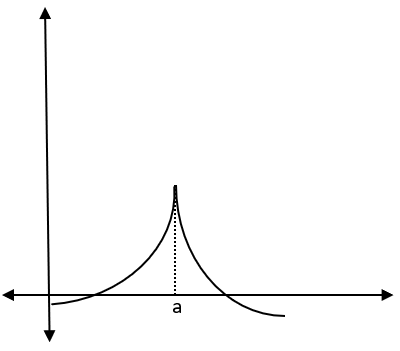
Yukarıdaki grafikte a noktasına sağdan ve soldan olmak üzere iki farklı teğet çizebiliyoruz. Bir noktanın sadece bir adet teğeti olabiliyordu.Yani fonksiyonumuzun a noktasındaki türevini (eğimini) bulabilmemiz için Fonksiyonun o noktada keskin bir şekilde dönmemesi-değişmemesi gerekiyor. Eğrimiz o noktada yumuşak olmalı.
4. Eğime tan a demiştik. Son olarak tan a değerinin tanımsız, belirsiz olduğu yerleri tanım kümemizden çıkarmamız gerekiyor.
olduğundan sabit bir fonksiyonun tanımlı olduğu her noktada eğiminin 0 olduğunu söyleyebiliriz.
Peki her seferinde bu formülü uzun uzun kullanmamız mı gerekiyor?
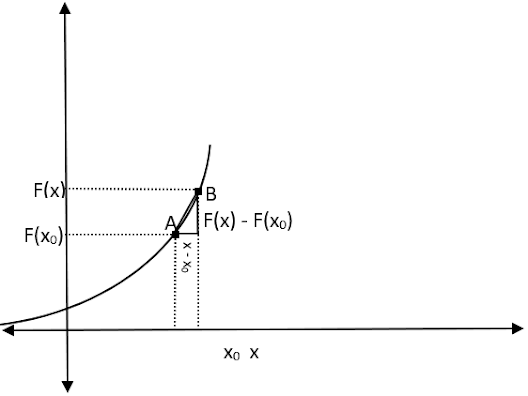
Bulduğumuz türevin tanımından herhangi bir fonksiyonun x noktasındaki türevini bulursak kısa bir türev alma kuralı oluşturabiliriz. Ancak bizim tanımladığımız türevde x0 gibi bir nokta yerine direk x noktası alınırsa 0/0 belirsizliği oluşuyor ve giderilemiyor bu sebeple paydayı 0 yapmayacak bir tüev tanımı oluşturmamız gerekiyor.
Paydayı 0 yapan x – x0 değerine h dersek x yazdığımızda belirsizlikten bir nebze kurtulmuş oluyoruz.
x – x0 = h eşitliğinde x değişkenini x0 ‘a doğru yaklaştırırsak h değeri 0 a yaklaşacağından yeni tanımımız;
TÜREV NEDİR? İspatı
tanımımızı biraz daha daraltmamız gerekiyor. Hepimiz F(x) = x2 gibi bir fonksiyonun türevinin 2x olduğunu biliyoruz.bir fonksiyonun türevini bukadar kısa şekilde bulmamızı sağlayacak tanıma ulaşmak için yukardaki tanımı F(x) = xn gibi derecesi bilinmeyen bir fonksiyonda uygularsak elimize daha kısa bir tanım geçecektir. ( n ∈ N )
F: R => R , F(x) = xn ( n ∈ N )
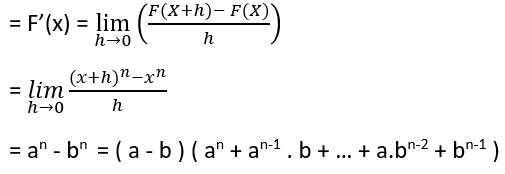
Eşitliğinden bunu bulabiliriz. 1. toplama kadar 0, 2. ‘ye kadar 1 x şeklinde gidiyor. Yani xn-1 ‘e ancak n. terimde ulaşabiliriz.
Yani herhangi bir n. dereceden x değişkeninin türevi n. xn-1 bulunuyor.
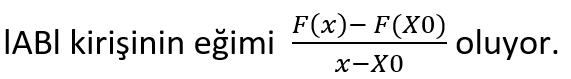
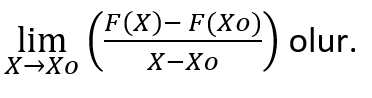
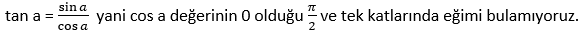
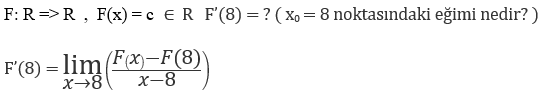
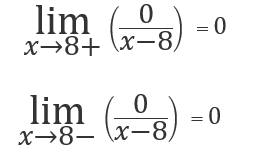
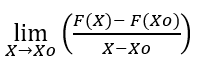
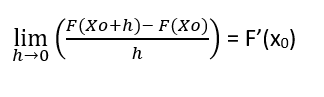
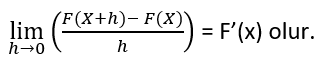
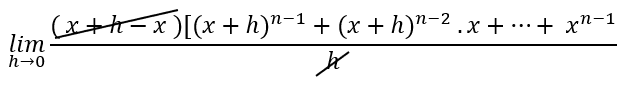
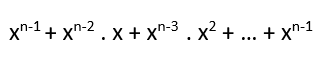
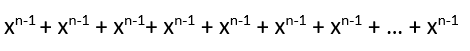
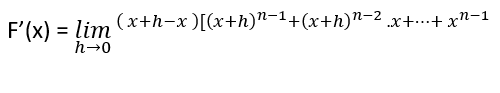
Teşekkür ederim. Şimdi türevin mantığını daha iyi anladım.
Ben teşekkür ederim zaman ayırıp okuduğunuz için.