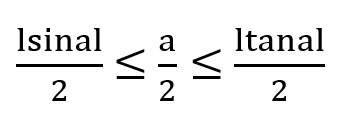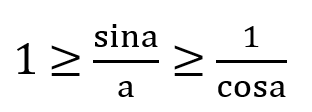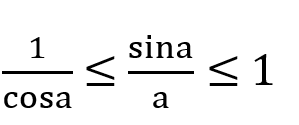Sinx/x NEDEN 1 ?

Önceki yazımızdaki arada kalma teoremi yardımı ile ispatlayacağımız bu teoremin ispatını anlamak için o teoremi bilmemiz gerekiyor. Arada kalma – Sandviç – Sıkıştırma teoremi olarak bilinen bu teoremin ispatına ulaşmak için buraya tıklayabilirsiniz.

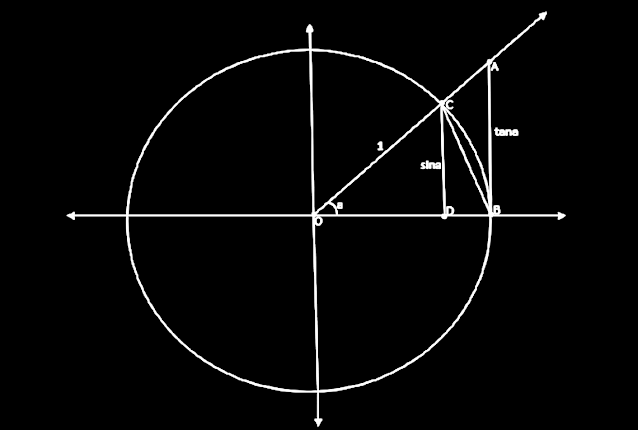
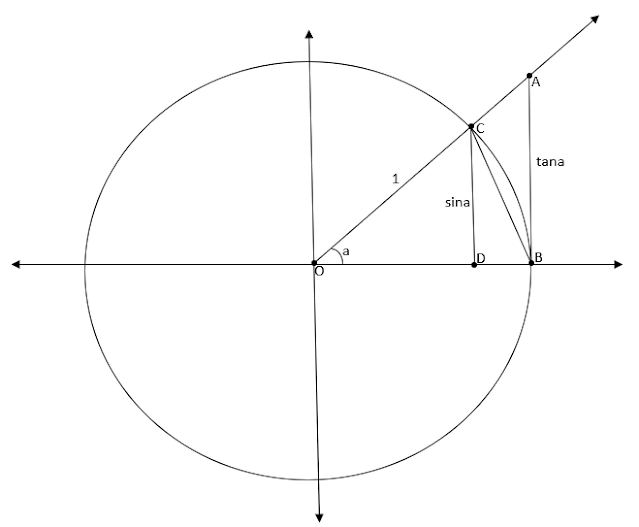
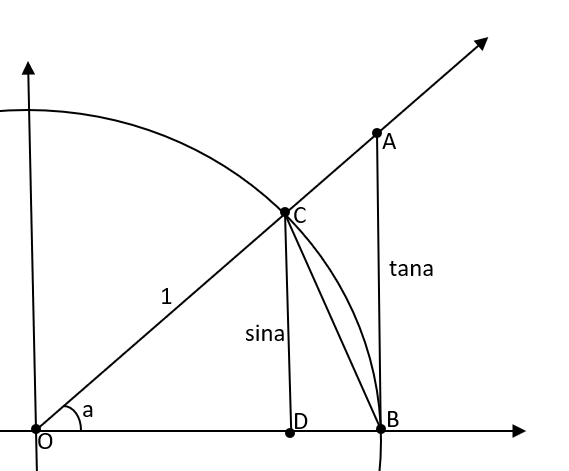
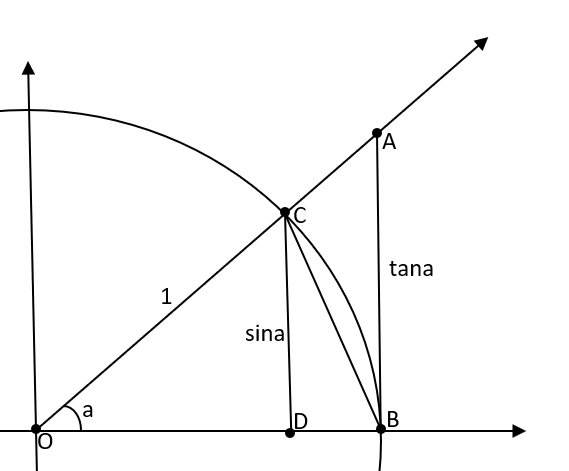
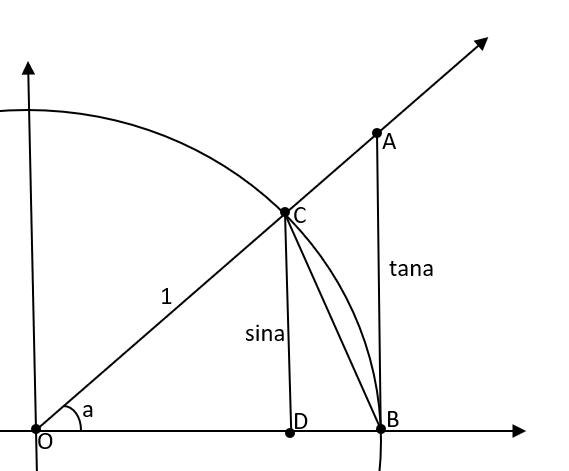
Bu teoremi ispatlamak için birim çemberden yardım alacağız.

Sinüs fonksiyonu karşı kenarın hipotenüs ‘e oranı olduğundan lCDl kenarının uzunluğu sina olur. Tanjant fonksiyonu da tanımı gereği karşı kenarın komşu kenara oranı olduğundan lABl kenarının lOBl kenarına oranı olacaktır. Çemberimiz birim çember olduğundan lABl kenarının uzunluğu tana olacaktır.

Amacımız lCOBl yayının alanının lOCBl üçgeninin alanı ile lOABl üçgeninin alanı arasında bir değer aldığını göstermektir. Bunu gösterdiğimizde arada kalma teoremini uygulayacağız.

İlk olarak lOCBl üçgeninin alanını bulalım. Taban.Yükselik/2 formülümüz den lOCBl üçgeninin alanı:

sina.1/2 olur. 

Şimdi ise lOABl üçgeninin alanını bulalım. Taban.Yükselik/2 formülümüzden lOABl üçgeninin alanını:

1.tana/2 olur.

Şimdi ise daire dilimimizin alanını bulalım. 

lCOBl Daire diliminin alanı: lOCBl üçgeninin alanından büyük, lOABl üçgeninin alanından küçük olduğundan aşağıdaki gibi bir eşitsizlik yazabiliriz. 

Her iki tarafı da 2/sina ile çarparsak:

Sinüs fonksiyonumuzu 1. ve 4. bölgede incelememiz gerekir. 1. Bölgede sina ve a pozitif olduğundan mutlak değerden pozitif çıkar. 4. Bölgede ikisi de negatif olduğundan yine pozitif çıkar. Şimdi mutlak değerleri kaldıralım ve eşitsizliğimizi ters çevirelim. (okun yönü değişeceğinden:)

Şimdi arada kalma teoremini uygularsak:

Sinx/x’in 1’e eşit olduğunu ispatlamış oluruz.

Yorumlarınız bizim için çok değerli. Lütfen yorum yapmayı unutmayın. Daha fazla içerik için Anasayfa’ya gidebilir yada İletişim bölümünden benim ile iletişime geçebilirsiniz.