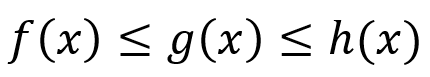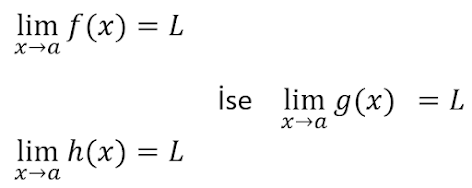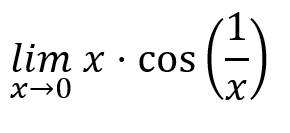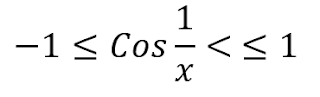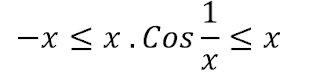Sıkıştırma sandviç arada kalma teoremi ispat – sıkıştırma sandviç arada kalma teoremi ispat
Yukarıdaki gibi bir eşitsizlikte f(x) ve g(x) fonksiyonlarının herhangi bir a noktasında limit değerleri aynı ise aralarında kalan g(x) fonksiyonunun da herhangi bir a noktasında limit değeri de diğer iki fonksiyonun limit değerine eşittir. Bu teorem genellikle trigonometrik fonksiyonların limitinde belirsizlik çıkması durumunda kullanılan bir teoremdir.
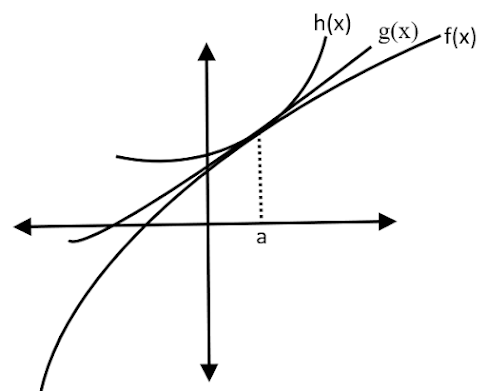
olmak zorundadır. Bu teoremi geometrik olarak gösterecek olur isek:
(Sıkışan fonksiyon g(x) fonksiyonudur.) h(x) ve f(x) fonksiyonları a noktasında aynı değere sahip ise g(x) fonksiyonu da a noktasında aynı değere sahip olmak zorundadır. Sıkışma teoremini daha iyi anlayabilmemiz için bir örnek soruyu inceleyelim.
SIKIŞTIRMA – SANDWİCH TEOREMİ ÖRNEK
İfadesinin limit değerini inceleyelim. x yerine 0 yazdığımızda 0 . Cos ( 1/0 ) olacağından belirsizlik ortaya çıkar. Sıkıştırma teoreminden başka uygulayabileceğimiz bir şey olmadığından sıkıştırma teoremi ile çözelim. Cos ( 1/x ) fonksiyonunun [ -1,1 ] kapalı aralığında olduğunu biliyoruz.
Limitimiz deki x . Cos ( 1/x ) ifadesini elde etmek için yukarıdaki eşitsizliği x ile çarpalım.
Sıkıştırma teoremine göre -x ‘in, 0 ‘a giderken ki limit değeri x ‘in, 0 ‘a giderken ki limit değerine eşit ise x . Cos( 1/x ) ifadesinin de 0 ‘a gider iken ki limiti diğer iki limitin sonucuna eşit olmalıdır.
Bu teorem bize limit konusunda trigonometrik ifadeler işin içine girdiğinde ( Genellikle trigonometrik ifadeler. ) birçok yerde kolaylıklar sağlamaktadır. Daha sonraki yazılarımızda limit değerinin 0 ‘a gitmesi halinde sinx/x ifadesinin 1 ‘e eşit olduğunu sıkıştırma, sandviç yada arada kalma teoremi olarak bilinen bu teorem yardımı ile ispatlayacağız.
Yorumlarınız bizim için çok değerli. Lütfen yorum yapmayı unutmayın. Daha fazla içerik için Anasayfa’ya gidebilir yada İletişim bölümünden benim ile iletişime geçebilirsiniz.