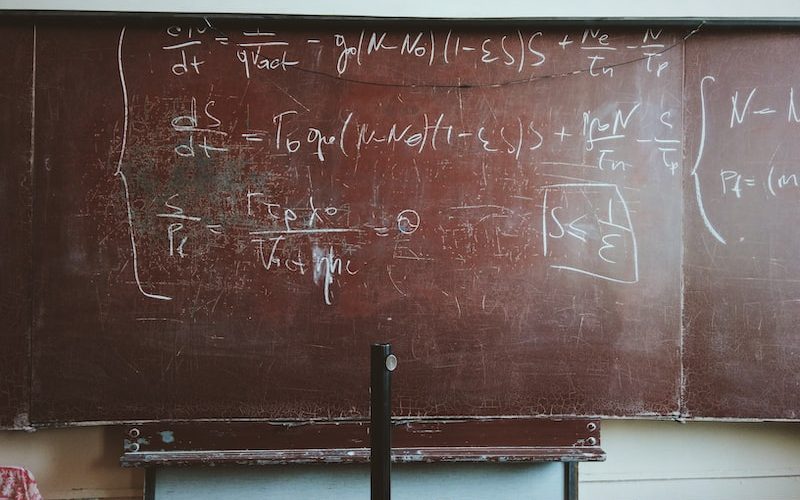Matematiksel analizde, artış teoremi kritik bir kavramdır. Bu teorem, sürekli bir fonksiyonun belirli bir aralıkta her noktada artan veya azalan olduğunu gösterir. Bu makalede, artış teoremi hakkında daha ayrıntılı bilgi verilecek ve nasıl kullanıldığı anlatılacaktır.
Artış teoremi, bir fonksiyonun türevinin pozitif veya negatif olduğu bir noktanın, bu fonksiyonun artan veya azalan olduğu anlamına geldiğini söyler. Basitçe söylemek gerekirse, eğer bir fonksiyonun türevi sıfırdan büyükse, o fonksiyon artan bir şekilde davranır. Tersine, eğer türev sıfırdan küçükse, fonksiyon azalır. Özetle, artış teoremi fonksiyonun değişimini analiz etmemizi sağlar.
Artış teoreminin uygulama alanları oldukça geniştir. Özellikle ekonomi, fizik ve mühendislik gibi disiplinlerde sıklıkla kullanılır. Örneğin, gelirin zamanla artması veya azalmasıyla ilgilenen bir ekonomist, artış teoremini kullanarak bu değişimi analiz edebilir. Aynı şekilde, bir mühendis, bir sürecin hızını veya gücünü hesaplarken artış teoreminden yararlanabilir.
Artış teoremi, matematiksel analizin temel taşlarından biridir ve çeşitli matematiksel kanıtlara dayanır. Bu teorem, bir fonksiyonun davranışını anlamamızı sağlar ve matematiksel modellemelerde önemli bir araçtır. Uygulamalarının yanı sıra, artış teoremi öğrencilerin matematiksel düşünce becerilerini geliştirmelerine de yardımcı olur.
artış teoremi matematiksel analizin önemli bir parçasıdır. Bir fonksiyonun artan veya azalan olduğunu belirlemek için türeviyle ilişkilendirilen bu teorem, birçok alanda uygulanmaktadır. Matematiksel modellerin oluşturulmasında kullanılan artış teoremi, değişimin analizinde bize rehberlik eder ve matematiksel düşünce becerilerimizi geliştirir.
Matematiksel Analizdeki Artış Teoremi: Temel İlke ve Uygulamalar
Matematiksel analiz, karmaşık problemleri çözmek için kullanılan önemli bir matematik dalıdır. Bu alanda birçok teorem ve prensip bulunmaktadır. Bu makalede, matematiksel analizin temel teoremlerinden biri olan Artış Teoremi’ne odaklanacağız. Artış Teoremi, fonksiyonların artış davranışını inceleyen ve integral hesaplamalarında kullanılan bir ilkedir.
Artış Teoremi, bir fonksiyonun sürekli olduğu bir aralıkta türevlenebilir olduğunu varsayar. Bu teorem, fonksiyonun integralini hesaplarken, türevin değerine dayanarak sonuçları tahmin etmemizi sağlar. Temel olarak, bir fonksiyonun artış hızının integralini alarak, fonksiyonun toplam artışını belirleyebiliriz.
Bu teoremin uygulama alanları oldukça geniştir. Örneğin, fizikteki hareket problemlerinde, yüzey alanının hesaplanması gereken geometri problemlerinde ve maliyet analizlerinde Artış Teoremi sıkça kullanılır. Aynı zamanda, ekonomi, istatistik ve mühendislik gibi birçok disiplinde de yaygın olarak kullanılan bir ilkedir.
Artış Teoremi’nin anlaşılması ve uygulanması, matematiksel analizdeki temel yeteneklerden biridir. Bu teorem, integral hesaplamalarında hızlı ve doğru sonuçlar elde etmemizi sağlar. Ek olarak, bazı problemlerin çözümünde Artış Teoremi’nin kullanılması, zaman ve kaynak tasarrufu sağlayabilir.
Matematiksel Analizdeki Artış Teoremi, fonksiyonların artış davranışını inceleyen ve integral hesaplamalarında kullanılan önemli bir ilkedir. Uygulama alanları oldukça geniş olduğundan, matematiksel analizi öğrenenler için temel bir kavramdır. Artış Teoremi, matematiksel analizin güçlü bir aracı olarak, karmaşık problemleri daha kolay anlamamızı ve çözebilmemizi sağlar.
Artış Teoremi: Limitlerin Sınırlarını Zorlayan Bir Araç
Matematik dünyasında, artış teoremi limit kavramının derinliklerine inen güçlü bir araç olarak karşımıza çıkar. Bu teorem, limit problemlerini çözmede önemli bir rol oynar ve matematiksel analizde sıklıkla kullanılır. Artış teoremi, fonksiyonların davranışını anlamak için kullanılan temel bir prensiptir ve limitleri daha iyi anlamamızı sağlar.
Artış teoremi, basit bir şekilde ifade edilebilir: Eğer belirli bir aralıkta sürekli bir fonksiyonun değeri pozitif ise, o zaman bu fonksiyonun artış yapacağı bir nokta vardır. Aynı şekilde, eğer fonksiyonun değeri negatifse, azalacağı bir nokta bulunur. Yani, bir fonksiyonun artış hızının veya azalış hızının sıfır olduğu bir nokta kesinlikle var olacaktır.
Bu teoremin pratikteki önemi oldukça büyüktür. Özellikle fizikte ve mühendislikte doğal olayları ve sistemleri analiz etmek için kullanılır. Örneğin, bir nesnenin hızını ve ivmesini hesaplarken artış teoremini kullanırız. Aynı zamanda ekonomi, istatistik ve diğer bilim alanlarında da geniş uygulama alanı bulur.
Artış teoremi, limitlerin sınırlarını zorlamanın yanı sıra analitik düşünce ve problem çözme becerilerimizi geliştirir. Bir fonksiyonun davranışını anlamak için türevleri ve integral hesaplamaları kullanırız. Bu sayede, matematiksel modelleri oluştururken gerçek dünya problemlerini daha iyi anlayabiliriz.
artış teoremi matematiksel analizin önemli bir parçasıdır ve limitlerin sınırlarını keşfetmek için güçlü bir araç olarak işlev görür. Fonksiyonların artış ve azalış hızını anlamamızı sağlar ve gerçek dünya problemlerini çözmek için kullanılır. Bu teorem, matematiği daha derinlemesine kavramak isteyenler için heyecan verici bir konudur ve matematiksel düşünce becerilerini geliştirmeye yardımcı olur.
Matematiksel Analizde Artış Teoremi: Değişim Hızının Sırları
Matematiksel analiz, matematiksel yapıları ve süreçleri anlamak için kullanılan temel bir araçtır. Bu alanda birçok teorem ve kural bulunur, bunlardan biri de artış teoremidir. Artış teoremi, değişim hızını açıklayarak, bir sistemin ne kadar hızlı değiştiğini belirlememize yardımcı olur.
Artış teoremi, bir fonksiyonun türevini kullanarak değişim oranını hesaplar. Bir fonksiyonun türeviden yararlanarak, o noktadaki eğimi veya değişim hızını ölçebiliriz. Birçok gerçek dünya probleminde, değişim hızının anlaşılması önemlidir. Örneğin, bir aracın hızı, bir şirketin geliri veya bir popülasyonun büyüklüğü gibi pek çok örnekte değişim hızı bilgisi gerekmektedir.
Artış teoremi, integral hesaplama ve türev teorisiyle yakından ilişkilidir. İntegral hesaplama, bir fonksiyonun alanını veya toplam değişimini hesaplamak için kullanılırken, türev teorisi değişimin nasıl gerçekleştiğini anlamamıza yardımcı olur.
Değişim hızını anlamak, birçok alanda büyük önem taşır. Finansal piyasalarda, hisse senetlerinin değeri veya faiz oranlarının değişimi gibi faktörler, yatırımcıların kararlarını etkiler. Bilimsel araştırmalarda, değişim hızı, bir fenomenin nedenini ve sonucunu anlamamıza yardımcı olur.
Artış teoremi, matematiksel analizin temel taşlarından biridir ve sayısız uygulama alanı vardır. Değişim hızının sırlarını keşfetmek, hem matematiksel anlayışımızı genişletirken hem de günlük hayatta karşılaştığımız problemleri çözmemize yardımcı olur. Matematiksel analizin bu önemli kavramını anlamak, birçok disiplindeki başarılarımızın temelini oluşturur ve bizi gelecekteki zorluklara hazırlar.
Matematiksel analizin artış teoremi üzerinde düşünmek, değişimin doğasını anlamak için önemlidir. Bu teorem, karmaşık süreçleri basitleştirir ve bize değişimin nasıl gerçekleştiğini gösterir. Değişim hızını anlamak, günlük hayatta karşılaştığımız problemleri daha iyi çözmek için bizi donatır ve bilimsel keşiflerde yeni kapılar açar.
İleri Matematikte Gizli Güç: Artış Teoremi’nin Şaşırtıcı Sonuçları
Matematik, birçok insan için karmaşık ve anlaşılması zor bir konu gibi görünebilir. Ancak, matematiksel dünyanın derinliklerine indiğinizde, sizi şaşırtacak kadar ilginç ve güzel sonuçlarla karşılaşabilirsiniz. İşte ileri matematikteki gizli güçlerden biri olan “Artış Teoremi”nin şaşırtıcı sonuçları.
Artış Teoremi, sürekli fonksiyonların davranışını analiz etmek için kullanılan bir teorem olarak bilinir. Bu teorem, herhangi bir sürekli fonksiyonun belirli bir aralıktaki artış miktarını tanımlar. Bu şekilde, fonksiyonun eğrisi üzerindeki değişimleri ölçmek ve analiz etmek mümkün olur.
Bu teorem, çok çeşitli uygulamalara sahiptir. Özellikle ekonomi, fizik, istatistik ve mühendislik gibi alanlarda yaygın olarak kullanılır. Örneğin, bir işletme sahibi, satışlarının zamanla nasıl arttığını veya azaldığını anlamak için bu teoremi kullanabilir. Veya bir fizikçi, bir parçacığın hızının nasıl değiştiğini incelemek için Artış Teoremi’ni uygulayabilir.
Ancak, Artış Teoremi’nin gerçekten şaşırtıcı sonuçlar sunduğu yer, matematiksel analizin derinliklerine indiğinizde ortaya çıkar. Örneğin, bazı fonksiyonlar için bu teorem, beklenmedik sonuçlar üretebilir. Fonksiyonlar arasında keskin zirveler veya uçurumlar bulunabilir. Ayrıca, Artış Teoremi’nin belirli koşullar altında nasıl genelleştirilebileceği ve farklı matematiksel kavramlarla ilişkilendirilebileceği de araştırma konularıdır.
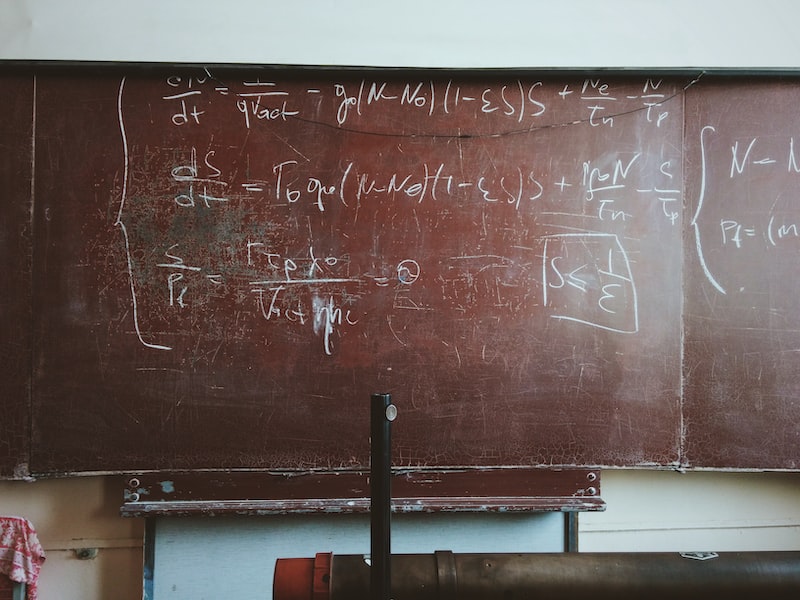
Bu gizli güçlere sahip olan Artış Teoremi, matematiğin sadece sayılarla uğraşan bir disiplin olmadığını gösterir. Matematik, soyut düşünme, modelleme ve analitik düşünme becerilerini gerektiren bir bilimdir. Bu nedenle, ileri matematikteki gizli güçleri keşfetmek, matematiksel anlayışınızı derinleştirmenize ve düşünsel becerilerinizi geliştirmenize yardımcı olabilir.
Artış Teoremi, matematiksel analizin derinliklerinde gizlenen güçlü bir araçtır. Bize fonksiyonların değişimini analiz etme ve beklenmedik sonuçlar keşfetme imkanı sunar. Matematiğin güzelliği ve şaşırtıcılığı, bu tür teoremlerin ortaya koyduğu sonuçlarla açığa çıkar. İleri matematikteki gizli güçlerden biri olan Artış Teoremi, matematikseverler için sürekli keşfedilecek yeni bir dünyanın kapılarını aralar.