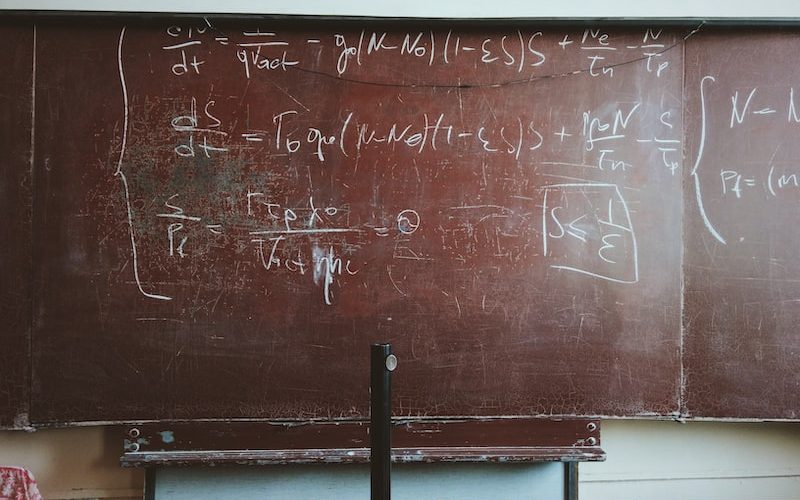Akışlar ve hareketli sistemler, fiziksel olayları anlamamızı sağlayan önemli bir araçtır. Diverjans teoremi, akışların bir bölgedeki değişimini analiz ederken kullanılan bir matematiksel kavramdır. Bu makalede, diverjans teoreminin ne olduğunu ve nasıl kullanıldığını keşfedeceğiz.
Diverjans teoremi, vektör alanlarının akışını ölçmek için Gauss teoremini uygular. Bir vektör alanı, her bir noktada bir yöneticiye sahip olan bir alan olarak düşünülebilir. Diverjans ise bu alanın her noktadaki net çıkış veya giriş miktarını ifade eder. Yani, bir bölgedeki akışın içeri veya dışarı doğru olup olmadığını belirlememize yardımcı olur.
Bu teorem, bir kütle veya sıvının bir bölgeden diğerine nasıl hareket ettiğini anlamamızı sağlar. Örneğin, bir sıvının belirli bir hacmi terk ettiği veya içine girdiği durumları analiz edebiliriz. Diverjans teoremi, sıvı dinamiği, elektromanyetizma ve akışkanlar mekaniği gibi birçok fiziksel alanda yaygın olarak kullanılır.
Diverjans teoremi, matematiksel ifadesiyle de ifade edilebilir. Bir vektör alanının diverjansı, alanın parçacık akış hızlarının noktasal dağılımlarının toplamının hacimdeki artışa oranı olarak tanımlanır. Bu sayede, bir bölgedeki akışın net çıkış veya giriş miktarını hesaplayabiliriz.
diverjans teoremi, hareketli sistemlerin analizinde önemli bir araçtır. Fiziksel olayların anlaşılmasında ve akışların incelenmesinde kullanılır. Diverjans teoremi, matematiksel ifadesiyle akışın net miktarını hesaplamamızı sağlar. Bu kavram, birçok farklı alanda uygulama bulur ve akışlarla ilgili derinlemesine bir anlayış sağlar.
Diverjans Teoremi: Akışkanların Gizemli Matematiksel Yolu
Akışkanlar, doğamızın bir parçasıdır ve hayatımızın pek çok yönünü etkiler. Peki, bu akışkanların matematiksel olarak nasıl incelenebileceğini hiç merak ettiniz mi? İşte burada diverjans teoremi devreye girer. Diverjans teoremi, akışkanların hareketini ve değişimlerini analiz etmek için kullanılan bir matematiksel araçtır. Bu makalede, diverjans teoremi hakkında daha fazla bilgi alacak ve akışkanların gizemli matematiksel yolunu keşfedeceksiniz.
Diverjans teoremi, vektör alanlarıyla ilgilenen bir matematik dalı olan vektör analizinde kullanılır. Temel olarak, bir akışkanın belirli bir hacimdeki (V) kaynak veya süzgeçlere ne kadar akış yaptığını tanımlar. Bu teorem, akışkanların hareketini matematiksel bir ifadeyle ifade etmeyi mümkün kılar. Böylece, akışkanların özelliklerini anlamak ve analiz etmek daha kolay hale gelir.
Diverjans teoremi, Gauss teoremi olarak da bilinir. Bu teorem, bir kapalı yüzeyin üzerindeki akışkan akısının, içindeki kaynak veya süzgeçlerin toplam etkisini temsil ettiğini belirtir. Yani, akışkanın bir noktadan çıkan veya o noktaya giren toplam miktarını hesaplamak için kullanılır. Diverjans teoremi, akışkanların hareketinin anlaşılması ve modellemesi açısından büyük öneme sahiptir.
Diverjans teoremi, hem fizikte hem de mühendislikte geniş bir uygulama alanına sahiptir. Hava akışı, suyun hareketi, elektromanyetik alanlar gibi birçok doğal olgu, diverjans teoremiyle analiz edilebilir. Bu teorem, akışkanların davranışını matematiksel olarak açıklamak suretiyle, mühendislerin ve bilim insanlarının akışkan sistemleri üzerinde daha iyi kontrol sağlamalarına yardımcı olur.
diverjans teoremi akışkanların gizemli matematiksel yolunu aydınlatır. Akışkanların hareketini, kaynak ve süzgeçlerle ilişkilendirerek matematiksel bir ifadeye döker. Bu teorem, akışkanların analizini kolaylaştırarak mühendislik ve fizik alanında büyük öneme sahip olur. Akışkanlarla ilgili çalışmalar yaparken diverjans teoremini anlamak, daha karmaşık sorunları çözmek için kritik bir adımdır.
Matematik ve Fizikteki Hayati Rolüyle Diverjans Teoremi
Matematik ve fizik, doğanın temel prensiplerini anlamamızı sağlayan disiplinlerdir. Bu iki alanın kesişim noktasında, birçok önemli teoremi bulunmaktadır. Bu makalede, matematik ve fizik dünyasında hayati bir role sahip olan diverjans teoreminden bahsedeceğiz.
Diverjans teoremi, çok boyutlu vektör alanlarının akışını inceleyen bir teoremdir. İlk olarak, İskoç matematikçi ve fizikçi olan James Clerk Maxwell tarafından ortaya atılmıştır. Bu teorem, Gauss teoremi veya Gauss’un yüzey integral teoremi olarak da bilinir. Diverjans teoremi, bir hacmin sınırlarındaki akışın hacme giren veya hacmden çıkan miktarını hesaplamamıza izin verir.
Bu teorem, fiziksel sistemlerdeki akış problemlerinin analizinde büyük öneme sahiptir. Özellikle akışkanlar mekaniği, elektromanyetizma ve termodinamik gibi alanlarda kullanılır. Örneğin, akışkanlar mekaniğinde, bir sıvının belli bir hacimden ne kadar akacağını veya hacme ne kadar madde gireceğini belirlemek için diverjans teoremi kullanılır.
Matematiksel açıdan, diverjans teoremi, vektör hesabının önemli bir aracıdır. Alan integrali ve yüzey integralini bağlantılı hale getirerek, fiziksel sistemlerin analizinde kullanılan matematiksel modellemelerde büyük kolaylık sağlar. Bu teorem, matematiksel çözümlerin daha etkili bir şekilde bulunmasını ve doğru sonuçlara ulaşmayı sağlar.
Diverjans teoremi, matematik ve fizik alanında öğrenim gören öğrenciler ve araştırmacılar için temel bir kavramdır. Doğru anlaşılması, karmaşık problemleri çözmek ve yeni keşifler yapmak için önemlidir. Ayrıca, bu teoremin uygulama alanları oldukça geniştir ve mühendislik, astronomi, jeoloji gibi birçok alanda da kullanılır.
matematik ve fizikteki hayati rolüyle diverjans teoremi, akış problemlerinin analizinde ve matematiksel modellemelerde önemli bir araçtır. Matematiksel ifadelerle ifade edilen bu teorem, doğanın temel prensiplerini anlamamızı sağlayarak, bilimsel ve teknolojik gelişmelere katkıda bulunur. Diverjans teoremi, matematik ve fizik dünyasının ayrılmaz bir parçası olup, araştırmacılar için sürekli ilgi odağı olmaya devam etmektedir.
Gauss’un Harika Keşfi: Diverjans Teoremi’nin Ardındaki Bilimsel Mucize

Matematik dünyasında, Gauss gibi dehaların keşifleriyle sık sık karşılaşırız. Bu makalede, Gauss’un harika bir keşfi olan ve fiziksel sistemlerin analizinde önemli bir rol oynayan Diverjans Teoremi’ni ele alacağız. Bu teorem, akışkanların hareketini anlamamıza ve çeşitli fiziksel özelliklerini hesaplamamıza yardımcı olan temel bir araçtır.
Diverjans Teoremi, vektör hesabının merkezi bir prensibi olarak bilinir. Bu teoreme göre, bir vektör alanının kapalı bir yüzeyin içinden geçen akısıyla, aynı vektör alanının hacim integrali arasında bir ilişki bulunur. Basitçe söylemek gerekirse, bir akı, bir yüzeyin içinden ne kadar “sızdığını” ya da “dışarı taştığını” belirler. Bu, fiziksel sistemlerin nasıl davrandığını anlamamız için son derece değerlidir.
Diverjans Teoremi, çeşitli fizik alanlarında geniş uygulama alanlarına sahiptir. Örneğin, elektromanyetizma alanında Maxwell denklemlerinin formülasyonunda, akışkan dinamiği ve gazların davranışının analizinde, ısı transferi problemlerinde ve daha birçok alanda kullanılır. Bu teorem, karmaşık matematiksel hesaplamalar gerektirebilir, ancak sonuçlar oldukça değerlidir.
Bu mucizevi keşif, Gauss’un bilimsel dehasının bir göstergesidir. Diverjans Teoremi, doğanın derinliklerindeki gizli prensipleri açığa çıkararak, fiziksel sistemlerin karmaşıklığını anlama yolunda önemli bir adımdır. Gauss’un bu keşfi, matematik ve fizik arasındaki güçlü bağlantıyı ortaya koymaktadır.
Gauss’un Diverjans Teoremi’ndeki harika keşfi, bilim dünyasında büyük bir etkiye sahiptir. Bu teorem, akışkanların hareketini ve fiziksel özelliklerini analiz etmek için vazgeçilmez bir araçtır. Gauss’un çalışmaları, matematik ve fizik arasındaki derin ilişkiyi ortaya koyarak, bilimsel ilerlemenin sınırlarını genişletmiştir. Diverjans Teoremi, onun bilimsel mucizesinin bir ifadesidir ve günümüzde hala aktif olarak kullanılan temel bir prensiptir.
Diverjans Teoremi: Alanın İçinde Saklı Matematiksel Hazine
Matematik, sayılar ve denklemlerle dolu bir evrende gizli hazineye benzer. Bu hazineyi keşfetmek için çeşitli teoremler kullanılır ve bu makalede, diverjans teoremi adı verilen bir matematiksel aracın gücünden bahsedeceğim.
Diverjans teoremi, vektör alanların hareketini anlamamıza yardımcı olan önemli bir kavramdır. Bir düzlemi veya uzayı dikkate alalım ve her noktada bir vektör alanı düşünelim. Bu vektör alanı, belirli bir yönde ne kadar “akış” olduğunu temsil eder. Diverjans teoremi, vektör alanının akışının toplam değişiminin, içinde bulunduğu bir hacmin sınırlarındaki akımların toplamına eşit olduğunu ifade eder.
Bu teorem, fizikte ve mühendislikte birçok uygulama alanına sahiptir. Örneğin, akışkanlar mekaniğinde, elektrik alanları ve manyetik alanlar gibi fiziksel alanlarda ve hatta finansal modellerde bile kullanılır. Diverjans teoremi, bu alanların karmaşıklığını basit bir şekilde ifade etmeye yardımcı olur ve hesaplamaları kolaylaştırır.
Diverjans teoremi, matematiksel analizde de büyük bir öneme sahiptir. İntegral hesabıyla ilişkilidir ve özellikle Gauss integralleri ve Stokes teoremiyle birlikte kullanıldığında güçlü sonuçlar elde edilir. Bu teorem, diferansiyel denklemlerin çözümünde ve matematiksel modellemelerde temel bir araç olarak kabul edilir.
diverjans teoremi, matematiğin derinliklerinde saklı olan bir hazine gibidir. Bu teorem, vektör alanların akışını anlamamızı sağladığı gibi birçok uygulama alanında da kullanılır. Matematiksel analizin temel araçlarından biri olan diverjans teoremi, matematiği anlamak ve gerçek dünyada kullanmak isteyenler için önemli bir konudur.