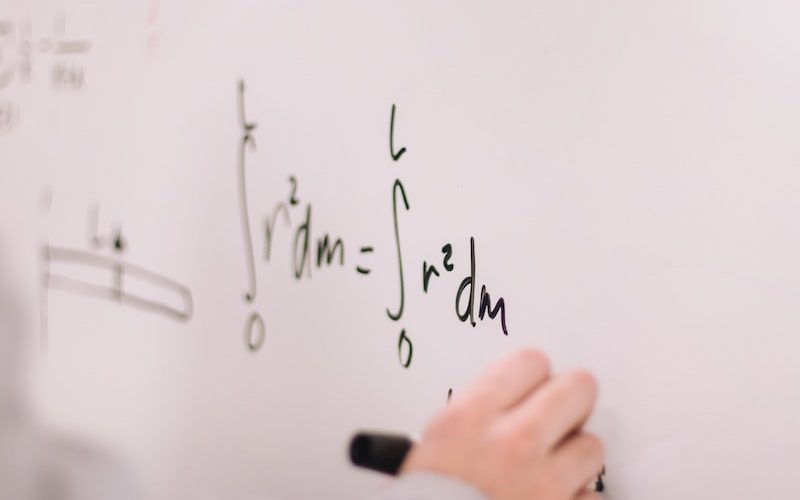Cebirsel geometri, matematiksel nesnelerin cebirsel yapılarıyla geometrik şekiller arasındaki ilişkiyi inceleyen bir alan olarak tanımlanır. Bu disiplinde, Grothendieck Bağlantılılık Teoremi önemli bir konumda yer alır. Bu makalede, Grothendieck Bağlantılılık Teoremi’nin ne olduğunu ve cebirsel geometri alanında nasıl kullanıldığını keşfedeceğiz.
Grothendieck Bağlantılılık Teoremi, Fransız matematikçi Alexandre Grothendieck tarafından ortaya atılmıştır. Bu teorem, bir cebirsel çeşidin (bir cebirsel denklemle tanımlanan geometrik bir nesne) “bağlantılı” olup olmadığını belirler. Bir çeşit bağlantılıysa, üzerindeki herhangi iki nokta arasında bir yol vardır; yolu keserek çeşidi parçalara ayırmak mümkün değildir. Bağlantısızsa, çeşit birden fazla bileşene ayrılabilir.
Bu teorem, cebirsel geometrinin birçok farklı alanında önemli sonuçlar sağlar. Örneğin, bir çeşidin bağlantılı olup olmadığını belirlemek, diğer cebirsel özelliklerini incelemek için önemli bir adımdır. Ayrıca, cebirsel geometrinin diğer dallarıyla olan ilişkileri anlamamızı sağlar.
Grothendieck Bağlantılılık Teoremi’nin kanıtı oldukça karmaşıktır ve burada detaylarına girmeyeceğiz. Ancak, bu teorem cebirsel geometri alanında büyük bir etkiye sahip olmuştur ve matematiksel araştırmalarda geniş bir uygulama alanı bulmuştur.
Grothendieck Bağlantılılık Teoremi, cebirsel geometrideki bağlantılılık kavramını tanımlayan önemli bir teoremdir. Bu teorem, çeşitli matematiksel araştırmalarda uygulanan ve cebirsel geometri ile ilgilenen araştırmacılar için temel bir araçtır. Cebirsel geometri alanının derinliklerine giren bu teorem, matematiksel düşünceye yeni kapılar açar ve gelecekteki çalışmalara rehberlik eder.
Matematik Dâhisi Grothendieck ve Cebirsel Geometriye Yaptığı Devrim
Matematik tarihinde nadiren karşılaşılan bir dâhi olan Alexandre Grothendieck, cebirsel geometri alanına yaptığı devrimle matematik dünyasını büyüledi. Grothendieck’in çalışmaları, matematiksel düşünceyi derinlemesine etkiledi ve sayısız açılım ve keşifle sonuçlandı.
Grothendieck, soyut cebiri ve topolojiyi birleştiren modern matematiğin temel taşlarından birini oluşturdu. Çalışmalarıyla, matematiksel nesneler arasındaki yapısal benzerlikleri ortaya çıkaran yeni bir yaklaşım geliştirdi. Bu bağlamda, cebirsel geometri alanında çığır açıcı bir rol oynadı.
Cebirsel geometri, matematiksel nesneleri cebirsel denklemlerle tanımlayan bir disiplindir. Grothendieck’in getirdiği yenilik, cebirsel geometriyi daha soyut bir seviyeye taşımaktı. Geleneksel olarak, cebirsel geometri, düzlemdeki noktaların eğriler ve yüzeylerle ilişkilendirilmesiyle ilgilenirken, Grothendieck soyut bir mekan kavramı geliştirerek bu sınırlamayı aştı. Böylece, matematikçiler, cebirsel nesneleri daha genel bir bağlamda inceleyebildiler.
Grothendieck’in çalışmaları, matematikteki önemli açık sorunların çözümünde kullanılan tekniklerin geliştirilmesine de yol açtı. Örneğin, Fermat’nın Son Teoremi gibi zorlu problemler, Grothendieck’in soyut cebir ve geometri arasındaki ilişkileri keşfetmesiyle daha iyi anlaşılabilir hale geldi.
Bu dâhinin yaklaşımı, matematik topluluğunda büyük bir etki yarattı. Grothendieck’in çalışmaları, matematikteki düşünce tarzını derinden etkiledi ve yeni yollar açtı. Onun mirası, matematiksel düşünceyi yeniden şekillendiren ve gelecekteki keşiflere ilham veren bir kaynak olarak kalacaktır.
Alexandre Grothendieck, matematik tarihinde eşsiz bir yer işgal eden bir dâhidir. Cebirsel geometriye getirdiği devrimci yaklaşımıyla, matematiksel düşünceye derinlik, kapsam ve özgünlük kazandırdı. Grothendieck’in çalışmaları, matematik dünyasında heyecan ve patlama yarattı ve bugün bile matematiksel keşiflerde rehberlik ediyor.
Sıradışı Bir Teorem: Grothendieck Bağlantılılık Teoremi Hakkında Her Şey
Grothendieck Bağlantılılık Teoremi, matematik camiasında büyük bir heyecan yaratmış ve birçok araştırmacının ilgisini çekmiştir. Bu sıradışı teorem, algebraik geometri ve cebirsel topoloji alanlarında önemli bir yer tutar. İşte Grothendieck Bağlantılılık Teoremi hakkında tüm detaylarıyla ele alacağımız bir makale:
Grothendieck Bağlantılılık Teoremi, 20. yüzyılın en etkileyici matematiksel keşiflerinden biri olarak kabul edilir. Alexandre Grothendieck tarafından formüle edilen bu teorem, karmaşık manifoldların topolojik özellikleriyle cebirsel yapıları arasında derin bir ilişki olduğunu göstermektedir. Bu bağlamda, teorem, cebirsel geometri ve cebirsel topoloji arasındaki köprüyü sağlamlaştırır.
Grothendieck Bağlantılılık Teoremi’nin temel fikri, bir varyete üzerindeki cebirsel vektör demetlerinin (vektör uzaylarının genelleştirmeleri) tek boyutlu toplamsal integralini kullanmaktır. Bu integral, varyetenin topolojik özelliklerini, cebirsel verilerle ilişkilendirir. Teorem, çeşitli topolojik ve cebirsel kavramların arasındaki bağlantıları açıklayarak matematiksel bir birlik sunmaktadır.
Grothendieck Bağlantılılık Teoremi’nin etkisi, cebirsel geometrinin temellerini sarsmış ve yeni bir bakış açısı sunmuştur. Teorem, birçok matematikçinin çalışmalarını etkilemiş ve çeşitli alanlarda uygulanabilirlik sağlamıştır. Özellikle cebirsel topoloji, diferansiyel geometri, sayı teorisi ve matematiksel fizik gibi disiplinlerde Grothendieck Bağlantılılık Teoremi’nin sonuçları büyük bir ilgi görmüştür.
Bu sıradışı teorem, matematik camiasında derin bir etki bırakmasının yanı sıra, zorluğuyla da tanınır. Matematiksel bilginin derinliklerine inen araştırmacılar için önemli bir zorluk oluştururken, aynı zamanda matematiksel düşünceye yeni ufuklar açma potansiyeli de taşır.
Grothendieck Bağlantılılık Teoremi, matematiksel dünyada dikkat çeken bir teoridir. Bu teorem, cebirsel geometri ve cebirsel topolojide önemli bir rol oynamaktadır ve matematiksel keşiflerin hız kazanmasına katkıda bulunmuştur. Grothendieck Bağlantılılık Teoremi’nin anlaşılması, matematik camiasının gelecekteki çalışmaları için önemli bir adım olacaktır.
Grothendieck Bağlantılılık Teoremi: Matematiğin Temellerini Sarsan Keşif
Matematik, insanlık tarihinin en önemli bilim dallarından biridir. İnsanoğlu, çağlar boyunca doğada gözlemlediği düzenleri anlamaya çalışmış ve matematikle bu düzenleri açıklamıştır. Bu süreçte matematikçiler, yeni teoremler keşfetmek için sınırları zorlamış ve bazen de paradigmayı değiştirecek çığır açıcı buluşlara imza atmışlardır.
Bu bağlamda, Alexandre Grothendieck’in ortaya koyduğu Grothendieck Bağlantılılık Teoremi, matematik dünyasında devrim niteliğinde bir keşiftir. Bu teorem, cebirsel geometri ile ilgilenenler arasında büyük heyecan yaratmış ve matematiğin temellerini derinden sarsmıştır.
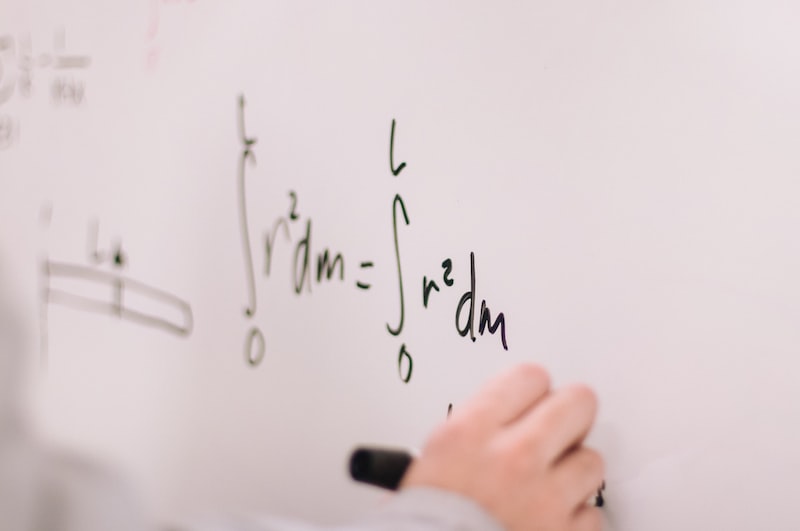
Grothendieck Bağlantılılık Teoremi, 20. yüzyılın ikinci yarısında Fransız matematikçi Alexandre Grothendieck tarafından geliştirilmiştir. Bu teorem, cebirsel geometrinin temel bir sorusunu ele alır: Bir şemasının (bir geometrik nesnenin cebirsel bir modeli) topolojik özelliklerini bağlantıları kullanarak nasıl anlayabiliriz?
Grothendieck Bağlantılılık Teoremi, şemaların topolojik özelliklerini açıklamak için kategoriler teorisi ve cebirsel geometri arasında derin bir ilişki kurar. Bağlantılar, geometrik nesneleri “bağlayan” matematiksel yapılar olarak düşünülür ve bu teorem, bu bağlantıların nasıl analiz edilebileceğini ortaya koyar.
Bu keşif, matematik dünyasında büyük bir etki yaratmıştır. Grothendieck Bağlantılılık Teoremi, matematikçilere yeni bir perspektif sunmuş ve daha genel bağlantı kuramlarının geliştirilmesine yol açmıştır. Ayrıca, teorem sayesinde farklı matematiksel disiplinler arasındaki ilişkiler daha iyi anlaşılmış ve matematiksel yapıların temelleri yeniden düşünülmüştür.
Grothendieck Bağlantılılık Teoremi matematik dünyasında bir dönüm noktası olmuştur. Bu keşif, cebirsel geometri ve kategoriler teorisi arasındaki ilişkiyi derinleştirmiş ve matematiksel düşüncenin sınırlarını genişletmiştir. Grothendieck’in bu teoremi, matematik alanında devrim niteliğinde bir adım olarak kabul edilmekte ve matematikçiler için hala önemli bir kaynak olarak değerini korumaktadır.
Karmaşık Matematiksel İlişkilerin Özeti: Grothendieck Bağlantılılık Teoremi
Matematik, birçok insan için karmaşık ve anlaşılması zor bir alan olarak görülebilir. Ancak, matematiksel düşünceyle ilgilenenler için, derin ve önemli ilişkilerin keşfedildiği heyecan verici bir alandır. Bu makalede, Grothendieck bağlantılılık teoremi gibi bir matematiksel konu hakkında size bilgi vereceğim.
Grothendieck bağlantılılık teoremi, Charles Ehresmann’ın çalışmalarından esinlenerek Alexandre Grothendieck tarafından formüle edilmiştir. Bu teorem, matematiksel nesnelerin birbirine bağlanabilmesi için gerekli olan koşulları inceler. Daha spesifik olmak gerekirse, Grothendieck bağlantılılık teoremi, matematiksel yapıların homotopik veya kohomolojik özellikleri arasındaki ilişkiyi açıklamaktadır.
Bu teorem, genellikle karmaşık cebirik geometri ve cebirsel topoloji çalışmalarında kullanılmaktadır. Söz konusu teorem, farklı matematiksel nesneler arasındaki bağlantıları belirlemeye yardımcı olur ve bu sayede matematiksel analizlerin ve kanıtların daha iyi anlaşılmasını sağlar.
Grothendieck bağlantılılık teoremi, matematiksel dünyada önemli bir yere sahiptir ve birçok alanın temel taşı olarak kabul edilir. Matematikçiler, bu teorem sayesinde derinlemesine çalışmalar yapabilir, yeni sonuçlar elde edebilir ve matematiksel düşünceye yeni yönler katabilirler.
Grothendieck bağlantılılık teoremi, matematiksel ilişkilerin anlaşılması ve araştırılması için önemli bir araçtır. Bu teorem, matematiksel nesnelerin birbirine bağlanabilmesi için gereken koşulları inceler ve bu sayede matematiksel analizlerin daha iyi yapılmasına yardımcı olur. Karmaşık matematiksel ilişkilerin özeti olan Grothendieck bağlantılılık teoremi, matematik dünyasında büyük bir etkiye sahiptir ve matematikçilere geniş bir keşif alanı sunar.