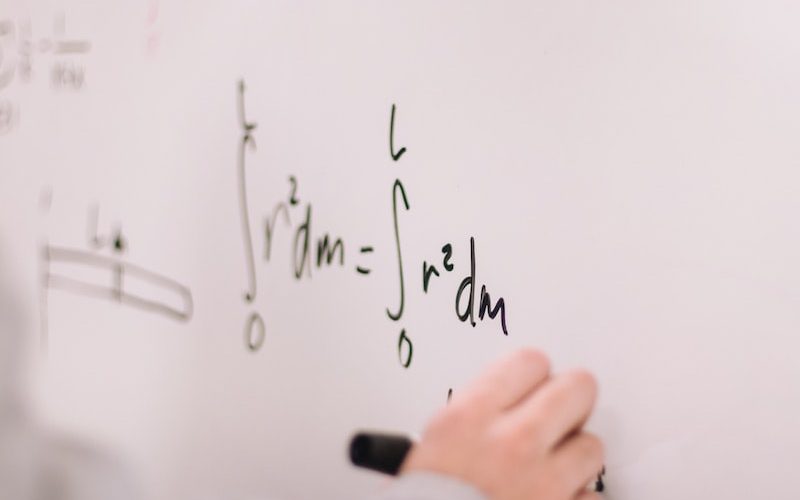Süreklilik teorisi, matematiksel analizin önemli bir alanıdır ve Hahn-Mazurkiewicz teoremi bu alandaki temel sonuçlardan biridir. Bu teoremle ilgili olarak, uzayın topolojik özellikleriyle ilgili önemli bir ilişki ortaya çıkar. Hahn-Mazurkiewicz teoremi, bir nokta kümesinin topolojik bir uzayda sürekli bir fonksiyon tarafından kaplanabilmesi için gerekli ve yeterli koşulları sağlar.
Bu teorem, içerdiği matematiksel kavramların yanı sıra, geniş uygulama alanlarına da sahiptir. Özellikle, coğrafya, ekonomi, fizik ve bilgisayar bilimleri gibi disiplinlerde kullanılır. Bu teorem, lokal ve global özellikler arasında bir bağlantı kurarak, süreklilik kavramının temel anlamını belirler.
Hahn-Mazurkiewicz teoremi, ayrık ve sürekli matematik arasındaki geçişin temsil edildiği bir köprü olarak düşünülebilir. Bir uzayın sürekli bir fonksiyonla kaplanılması, bu uzayın sürekli olma özelliğini vurgular. Bu teorem, sürekli fonksiyonların analizinde ve kavramsal modellerin oluşturulmasında önemli bir rol oynar.
Teoremin kanıtı oldukça karmaşık matematiksel kavramlar içermektedir ve genelde uzmanlar tarafından incelenir. Ancak, Hahn-Mazurkiewicz teoreminin temel fikri, herhangi bir nokta kümesinin sürekli bir fonksiyon tarafından kaplanabilmesi için gerekli olan şartları belirtmektedir.
Hahn-Mazurkiewicz teoremi, süreklilik teorisinde önemli bir yer tutan bir sonuçtur. Bu teorem, matematiksel analizin temel prensiplerinden birini açıklar ve farklı disiplinler arasındaki bağlantıları ortaya koyar. Matematiksel düşünceyi ve problem çözme yeteneğini geliştiren bu teorem, matematik dünyasının vazgeçilmez bir parçasıdır.
Matematikteki En Gizemli Teoremlerden Biri: Hahn–Mazurkiewicz Teoremi
Matematik dünyasında pek çok teorem ve prensip bulunmaktadır. Bunların içinde, özellikle karmaşık yapıları ve derin matematiksel anlamlarıyla bilinen gizemli teoremler de yer alır. Bu makalede, matematik tarihindeki en gizemli teoremlerden biri olan Hahn-Mazurkiewicz Teoremi’nden bahsedeceğiz.
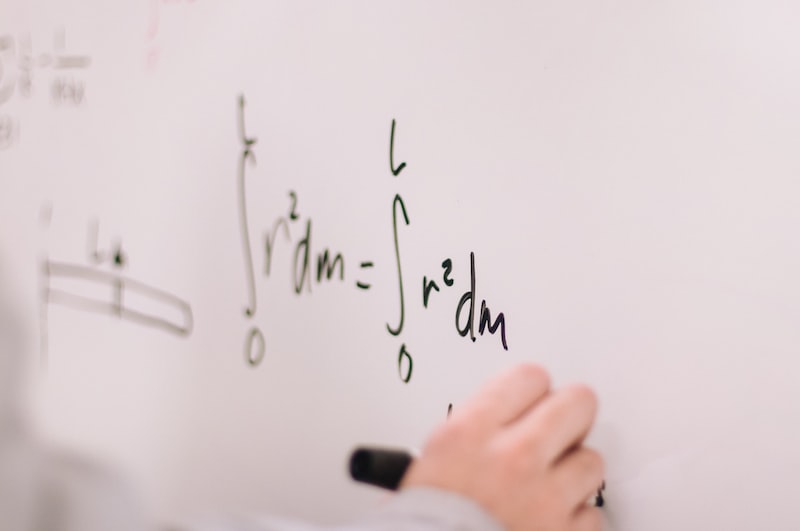
Hahn-Mazurkiewicz Teoremi, 20. yüzyılın başlarında Stanislaw Mazurkiewicz tarafından sunulan ve daha sonra Hans Hahn tarafından genelleştirilen bir teoremdir. Bu teorem, topoloji alanındaki önemli bir konuyu ele alır: Bir uzayın düzlemsel olarak çizilebilir olup olmadığını belirlemek.
Düzlemsel olarak çizilebilirlik, bir uzayın, üzerinde hiçbir kesişim olmayacak şekilde bir düzlem üzerine çizilebileceği anlamına gelir. Basit bir ifadeyle, bir kağıda çizdiğimiz bir şeklin, orijinal uzaydaki tüm noktaları kapsamasıdır.
Hahn-Mazurkiewicz Teoremi, bu özellikle ilgili olarak şu sonucu verir: Bir uzayın düzlemsel olarak çizilebilir olması için gerek ve yeter koşul, uzayın kompakt ve bağlantılı olmasıdır. Yani, bir uzayın her noktasını içeren ve kesintisiz bir çizgiyle temsil edilebilen bir düzlem üzerine çizilebilmesi için, o uzayın hem kompakt (sınırlı ve kapalı) hem de bağlantılı olması gerekmektedir.
Bu teorem, matematikçilerin uzayların özelliklerini anlamalarına ve analiz etmelerine yardımcı olur. Ayrıca topoloji, graf teorisi, fizik ve bilgisayar bilimleri gibi pek çok alanla da ilişkilendirilir.
Hahn-Mazurkiewicz Teoremi, matematiksel gizemi ve derinliğiyle büyüleyen bir teorem olarak kabul edilir. Bu teorem, matematikçilerin uzayları daha iyi anlayabilmeleri ve bu uzayların özelliklerini tanımlamaları için önemli bir araçtır.
Süreklilik ve Topoloji Arasındaki Bağlantıyı Keşfeden Teorem
Matematikte, süreklilik ve topoloji iki önemli kavramdır. Bu yazıda, süreklilik ve topoloji arasındaki bağlantıyı ortaya koyan bir teoremi ele alacağız. Bu teorem, matematiksel yapıları anlamamızı sağlayarak geniş bir uygulama alanına sahiptir.
Süreklilik ve topoloji, nesnelerin şekil değiştirmeden nasıl dönüşebileceğini inceleyen matematik dallarıdır. Süreklilik, bir fonksiyonun girdi ve çıktılarının yakın değerler arasında düzgün bir şekilde değiştiği durumu ifade eder. Topoloji ise cisimlerin uzayda nasıl konumlandığını ve birbirleriyle ilişkilerini inceler.
Bu bağlamda, “Süreklilik ve Topoloji Arasındaki Bağlantıyı Keşfeden Teorem” önemli bir adımdır. Bu teorem, bir fonksiyonun sürekli olabilmesi için gerekli ve yeterli koşulları belirler. Ayrıca, topolojik yapıların süreklilikle olan ilişkisini açıklar.
Teorem, matematiksel ifadelerden oluşur ve kanıtı kompleks olabilir. Ancak, temel fikri basitçe açıklanabilir. Bir fonksiyonun sürekli olabilmesi için, girdi ve çıktılarının topolojik yapılar arasındaki ilişkiyi bozmaması gerekir. Başka bir deyişle, yakın noktalardaki girdi değerleri, yakın noktalardaki çıktı değerlerine karşılık gelmelidir.
Bu teorem, fizikten ekonomiye, mühendislikten bilgisayar bilimine kadar birçok alanda uygulanabilir. Örneğin, sürekli optimizasyon problemleri çözerken veya verileri analiz ederken bu teoremden yararlanabiliriz. Ayrıca, sürekli dönüşümlerin ve deformasyonların incelendiği alanlarda da önemli bir rol oynar.
“Süreklilik ve Topoloji Arasındaki Bağlantıyı Keşfeden Teorem” matematiksel düşüncenin önemli bir ayağını oluşturur. Süreklilik ve topoloji arasındaki ilişkiyi anlamamızı sağlayarak daha derin bir anlayışa ulaşmamızı mümkün kılar. Bu teorem, matematiksel dünyanın temellerini sarsacak gücüne sahiptir ve birçok farklı disiplinde uygulanma potansiyeline sahiptir.
Hahn–Mazurkiewicz Teoremi: Sonsuz Boyutta Süreklilik Kavramının Sırrı
Hahn-Mazurkiewicz teoremi, sonsuz boyutta süreklilik kavramının temelini oluşturan bir matematiksel teoremdir. Bu teorem, topoloji alanında önemli bir yere sahiptir ve sürekli dönüşümlerin analiz edildiği birçok problemde kullanılır.
Bu teorem, 1920’lerde Hans Hahn ve Stanislaw Mazurkiewicz tarafından ortaya konulmuştur. Özünde, bu teorem sürekli fonksiyonların tanımıyla ilgilidir. Bir fonksiyonun sürekli olması için, girişin çok küçük değişikliklerine karşı çıktının değişmemesi gerekmektedir. Ancak, sonsuz boyutlu uzaylarda sürekli olmanın ne anlama geldiği karmaşık bir konudur.
Hahn-Mazurkiewicz teoremi, herhangi bir kompakt metrik uzayın sürekli bir fonksiyonla homeomorf olduğunu ifade eder. Yani, her noktası sürekli olarak diğerine eşlenebilir. Bu, sonsuz boyutlu uzayların da sürekli bir şekilde tanımlanabileceğini gösterir.
Teorem, başka bir deyişle, bir uzayı sürekli olarak bir başka uzayla eşleyen bir fonksiyonun varlığını garanti eder. Bu eşleme, birinci uzaydaki noktaların ikinci uzaydaki karşılıklarına gönderilmesiyle gerçekleşir. Bu sayede, sonsuz boyutlu uzaylarda süreklilik kavramının geçerliliği sağlanır.
Hahn-Mazurkiewicz teoremi, matematiksel analizde ve topolojide birçok uygulama alanı bulmuştur. Özellikle bağlantılılık, kompaklık ve homotopi gibi konuların incelendiği alanlarda sıkça kullanılır. Ayrıca, sürekli dönüşümlerin dinamik sistemlerdeki davranışlarının anlaşılmasında da büyük öneme sahiptir.
Hahn-Mazurkiewicz teoremi sonsuz boyutta süreklilik kavramının sırrını ortaya çıkaran önemli bir matematiksel teoremdir. Bu teorem, sürekli fonksiyonların tanımının sonsuz boyutlu uzaylarda da geçerli olduğunu gösterir ve matematiksel analizde ve topolojide birçok uygulama alanına sahiptir.
Topolojinin Temel Taşı: Hahn–Mazurkiewicz Teoremi
Matematik, bir dizi teorem ve kanıtla doludur. Bu teoremler, farklı alanlarda derinlemesine anlayış sağlar ve ileri düzey problem çözmede önemli bir rol oynar. Topoloji, matematiksel nesnelerin özelliklerini inceler ve birbirleriyle ilişkilerini araştırır. Bu disiplinin temel taşlarından biri olan Hahn-Mazurkiewicz teoremi, topolojinin merkezinde yer alır.
Hahn-Mazurkiewicz teoremi, bir uzayın kompaktlık özelliğini karakterize eder. Bu teorem, bir uzayın, sürekli bir eşlenikle bir eşbiçimlilik göstermesi durumunda kompakt olacağını belirtir. Bu, topolojik olarak ayrılamayan noktalardan oluşan bir uzayın, sürekli bir fonksiyon aracılığıyla diğer bir uzayla eşleşebileceği anlamına gelir.
Bu teorem, topolojide birçok uygulama alanına sahiptir. Örneğin, diferansiyel denklemlerin çözümünde, genelleştirilmiş kesirli boyutlu uzaylarda ve karmaşık analizde kullanılabilir. Ayrıca, Hahn-Mazurkiewicz teoremi, topolojik uzayların analitik veya sayısal yöntemlerle incelenmesinde de önemli bir rol oynar.
Hahn-Mazurkiewicz teoremi, matematiksel düşünce sürecinin ve mantığın kesiştiği noktada yer alır. Bu teorem, topolojik uzayların yapılarını anlamamızı sağlar ve bu alanda daha ileri araştırmalar için temel bir platform oluşturur. Ayrıca, Hahn-Mazurkiewicz teoremi, matematiksel kanıtlama becerilerimizi geliştirmemize yardımcı olur ve soyut düşüncenin gücünü gösterir.
Hahn-Mazurkiewicz teoremi, topolojinin temel taşlarından biridir ve matematiksel analizin merkezinde yer alır. Bu teorem, uzayların kompaktlık özelliğini karakterize eder ve birçok uygulama alanına sahiptir. Matematik camiasında geniş kabul gören bu teorem, ileri düzey problem çözmede ve topolojik uzayların incelenmesinde önemli bir rol oynamaktadır.