Hartogs Teoremi, karmaşık analiz alanında önemli bir teoremdir. Bu teorem, çok değişkenli kompleks fonksiyonların analiziyle ilgilenir ve daha genel olarak Cauchy-Riemann denklemlerinin genişletilmesini sağlar.
Hartogs Teoremi, bir fonksiyonun analitik olması için gerekli ve yeterli koşulları belirler. İki veya daha fazla değişkenli bir fonksiyonun analitik olabilmesi için, her değişkenin türevlenebilir olması yeterli değildir. Hartogs Teoremi, bu durumu açıklığa kavuşturur ve analitikliği sağlayan ek koşullar ortaya koyar.
Bu teorem, karmaşık analizdeki birçok temel sonucun elde edilmesinde kullanılır. Özellikle, tek bir değişkenli karmaşık analizin aksine, çok değişkenli karmaşık analizde Hartogs Teoremi’nin varlığı, fonksiyonların analitik genişlemelerinin varlığını garanti eder.
Hartogs Teoremi, analitik fonksiyonların sınırlı olma özelliğini de inceleyerek önemli sonuçlara ulaşır. Bir fonksiyonun sınırlı olması, o fonksiyonun analitik olmasına bağlıdır ve bu teorem tarafından kanıtlanır.
Karmaşık analizin bu temel teoremi, matematiksel fizikten mühendisliğe birçok alanda kullanılır. Özellikle elektromanyetizma, akışkanlar mekaniği ve kuantum mekaniği gibi alanlarda Hartogs Teoremi’nin sonuçları büyük önem taşır.
Hartogs Teoremi karmaşık analizin temel teoremlerinden biridir. Çok değişkenli fonksiyonların analitikliği ve sınırlı olma özellikleri ile ilgili önemli sonuçlar sağlar. Karmaşık analizdeki birçok alan için vazgeçilmez bir araçtır ve geniş uygulama alanlarına sahiptir.
Karmaşık Analizdeki Büyüleyici Keşif: Hartogs Teoremi
Karmaşık analiz, matematiksel bir disiplindir ve karmaşık sayılar üzerinde fonksiyonların davranışını inceler. Bu alanda yapılan keşifler, matematik dünyasında büyük ilgi uyandırırken yeni buluşlarla genişlemeye devam ediyor. Karmaşık analizin heyecan verici bir teoremi olan “Hartogs Teoremi”, bu alanda özel bir yere sahiptir.
Hartogs Teoremi, 20. yüzyılın başlarında Alman matematikçi Friedrich Hartogs tarafından formüle edilmiştir. Bu teorem, çok değişkenli fonksiyonların analizini ele alırken önemli bir rol oynar. Özellikle, bir fonksiyonun içinde tanımlı olmayan bir noktada sürekli olarak genişletilebileceğini belirtir.
Hartogs Teoremi’nin büyüleyici yanı, karmaşık analizin bazı temel prensiplerini ve kavramlarını kullanarak neredeyse sezgisel bir şekilde kanıtlanabilmesidir. Bir fonksiyonun tek bir noktada analitik olmaması durumunda bile, diğer noktalarda hala analitik olabileceği sonucuna varılır. Bu, matematikçilerin bir fonksiyonun analitikliğini incelemek için daha esnek bir yaklaşım benimsemesini sağlamıştır.
Hartogs Teoremi’nin önemi, karmaşık analiz alanında birçok uygulama bulmasına rağmen sadece bu teoremle sınırlı değildir. Özellikle, karmaşık analizin diğer temel teoremleriyle birlikte kullanıldığında, karmaşık fonksiyonların davranışını daha iyi anlamamızı sağlar. Bu, fizik, mühendislik ve bilgisayar bilimlerinde birçok alanda kullanışlıdır.
Hartogs Teoremi, karmaşık analizdeki büyüleyici keşiflerden biridir. Karmaşık sayılar üzerinde tanımlı olmayan noktalarda hala analitik olabileceğimizi göstermesi, matematikçiler için yeni kapılar açmıştır. Bu teorem, karmaşık analizin temel prensiplerini ve kavramlarını derinlemesine anlamamızı sağlayarak disiplinin ilerlemesine katkıda bulunmuştur.
Matematik Dünyasında Yankı Uyandıran Hartogs Teoremi
Matematik dünyasında, çeşitli teoremler ve matematiksel kavramlar sürekli olarak ilgi çekmektedir. Bu yıl tanıtılan ve büyük bir yankı uyandıran teoremlerden biri de Hartogs Teoremi’dir. Hartogs Teoremi, matematiksel analizde önemli bir yer tutan kompleks değişkenli fonksiyonlar alanında özellikle dikkat çekmektedir.
Hartogs Teoremi, Alman matematikçi Friedrich Hartogs tarafından 1915 yılında ortaya atılmıştır. Bu teorem, bir fonksiyonun karmaşık düzlemde analitik olup olmadığını belirlemek için kullanılan bir araçtır. Teorem, birkaç değişkenli fonksiyonlarla ilgilenen matematikçilerin çalışma alanına yeni bir bakış açısı getirmektedir.
Teorem, asıl olarak “bir karmaşık değişkenli bir fonksiyonun analitik olduğu bölgeye, daha fazla bir değişken ekleyerek aynı özelliklerin sürdürüldüğü” fikrine dayanmaktadır. Yani, eğer bir fonksiyon tek bir değişken üzerinde analitikse, bu fonksiyona ikinci bir değişken eklenerek tüm değişkenler üzerinde analitik hale getirilebilir.
Hartogs Teoremi’nin matematik camiasında büyük bir etkisi oldu. Birçok matematikçi, teoremin yeni araştırma alanlarına yol açabileceğini ve karmaşık değişkenli fonksiyonların analitik özelliklerinin daha iyi anlaşılmasına katkı sağlayabileceğini düşünmektedir. Ayrıca, teorem pratik uygulamaları olan diğer matematiksel disiplinlere de ilham vermiştir.
Hartogs Teoremi, matematik dünyasında büyük bir yankı uyandırmış ve kompleks değişkenli fonksiyonlar alanında önemli bir yer edinmiştir. Bu teorem, matematiksel analizde derinlemesine çalışma yapmak isteyenler için heyecan verici fırsatlar sunmaktadır. Hartogs Teoremi’nin ortaya koyduğu yeni bakış açısı, matematiksel araştırmalara yeni bir ivme kazandırmaktadır ve gelecekte daha da fazla keşif ve gelişmelere yol açabileceği umut edilmektedir.
Karmaşık Analizin Gizemli Köşelerinden Biri: Hartogs Teoremi
Karmaşık analizde, birçok önemli teorem ve kavramlar bulunmaktadır. Bu makalede, karmaşık analizin gizemli köşelerinden biri olan Hartogs Teoremi’nden bahsedeceğiz. Bu teorem, karmaşık fonksiyonlardaki analitiklik özelliklerini araştıran temel bir sonucu ifade eder.
Hartogs Teoremi, Alman matematikçi Friedrich Hartogs tarafından 1914 yılında ortaya konulmuştur. Temel olarak, bu teorem karmaşık düzlemdeki çok değişkenli fonksiyonların analitik genişlemesini ele almaktadır. Başka bir deyişle, sınırlı bir bölgede tanımlanan bir fonksiyonun tanım kümesini nasıl genişletebileceğimizi açıklar.
Teoremin ana fikri şudur: Sınırlı bir bölgede tanımlanan bir fonksiyon, bu bölgenin dışında da tanımlanabilir, ancak bu yeni tanımda yine analitik olmayabilir. Yani, bir fonksiyonun analitik olduğu bir bölgede, bu bölgenin dışındaki noktalarda analitik olma zorunluluğu yoktur.
Hartogs Teoremi’nin anlaşılması için bir örnek verelim. Diyelim ki, karmaşık düzlemde sınırlı bir daire içinde tanımlanan bir fonksiyonumuz var. Hartogs Teoremi’ne göre, bu fonksiyonu dairenin dışında da tanımlayabiliriz, ancak yeni tanım alanında analitiklik özelliğini koruması gerekmez.
Hartogs Teoremi’nin önemi, karmaşık analizdeki genişleme teoremlerinin ve analitik fonksiyonların davranışlarının anlaşılmasına yönelik bir kapı açmasıdır. Bu teorem, özellikle çok karmaşık sistemleri inceleyen araştırmacılar için büyük bir öneme sahiptir.
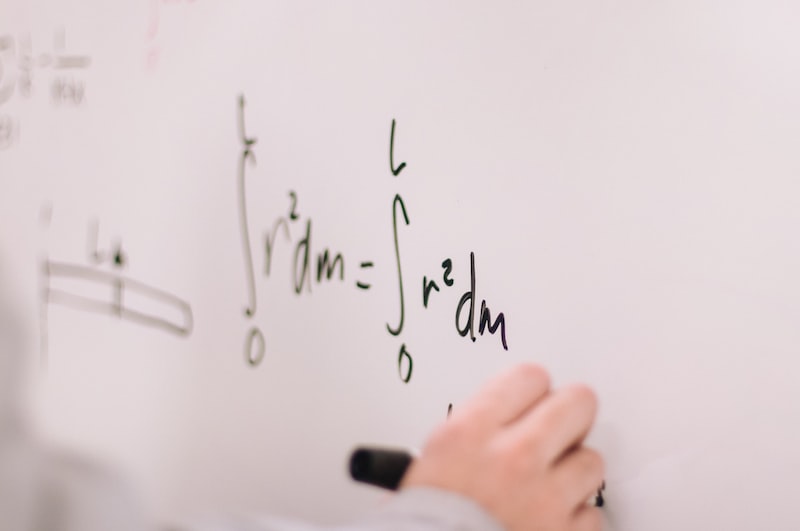
Hartogs Teoremi karmaşık analizin gizemli köşelerinden biridir ve karmaşık düzlemdeki çok değişkenli fonksiyonların analitik genişlemesini açıklamaktadır. Bu teorem, karmaşık analizdeki temel kavramları anlamak ve daha karmaşık yapıları incelemek için önemli bir araçtır.
İlham Veren Hartogs Teoremi: Karmaşık Analizin Sırlarını Açığa Çıkarıyor
Karmaşık analiz, matematiksel alanında önemli bir yer tutan ve karmaşık sayılarla ilgilenen bir disiplindir. Bu alanda yapılan çalışmalar, matematik dünyasına yeni perspektifler sunmakta ve bilim insanlarına çeşitli keşifler yapma imkanı sağlamaktadır. Bu bağlamda, Hartogs teoremi adını verdiğimiz özel bir sonuç, karmaşık analizdeki sırları açığa çıkaran önemli bir teorem olarak karşımıza çıkmaktadır.
Hartogs teoremi, 20. yüzyılın başında Alman matematikçi Friedrich Hartogs tarafından formüle edilmiştir. Bu teorem, karmaşık fonksiyonların analitik devamlılık özellikleriyle ilgilenmektedir. Özellikle çok değişkenli karmaşık fonksiyonlar üzerinde duran teorem, tek değişkenli teorilere benzer şekilde analiz yapmayı mümkün kılmaktadır.
Teorem, bir fonksiyonun analitik olarak genişletilebileceği bölgeyi belirleyen bir sınırlama sunmaktadır. Yani, bir fonksiyonun analitik olarak genişletilebildiği en büyük bölgeyi tanımlamaktadır. Hartogs’un bulduğu bu teorem, karmaşık analizdeki bazı önemli kavramların anlaşılmasını sağlamış ve matematikçilere yeni araştırma alanları sunmuştur.
Hartogs teoremi, matematik dünyasında büyük bir ilgiyle karşılanmıştır. Çünkü bu teorem, karmaşık analizin derinliklerine inme fırsatı vererek, daha önce çözülememiş sorunları ele almamızı sağlamaktadır. Ayrıca, teorem karmaşık analizdeki temel kavramları daha iyi kavramamızı ve daha karmaşık problemlerin çözümüne yönelik ipuçları sunmaktadır.
Hartogs teoremi karmaşık analizde büyük bir etkiye sahip olan ve matematiksel bakış açısını genişleten bir keşiftir. Bu teorem, karmaşık fonksiyonların analitik devamlılık özellikleri hakkında önemli bilgilere ulaşmamızı sağlayarak, matematik dünyasına yeni ufuklar açmaktadır. Hartogs’un çalışmaları, ilham verici niteliğiyle matematik camiasında saygıyla karşılanmaktadır ve gelecekteki araştırmalara da yön göstermektedir.
