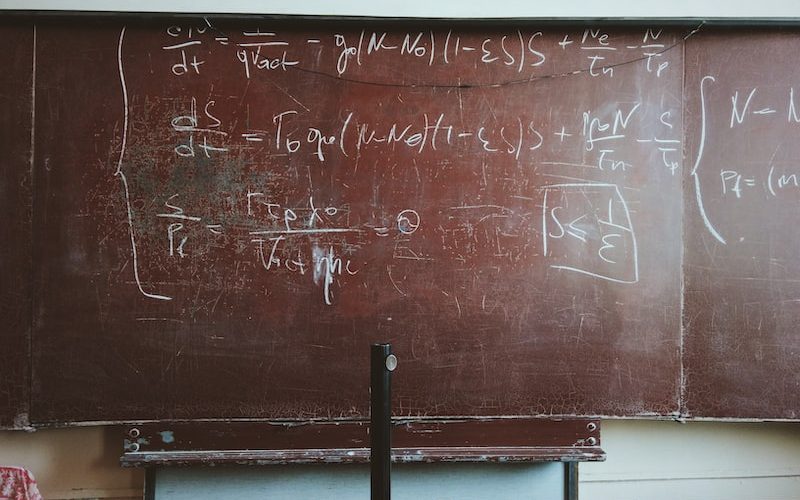Hellinger-Toeplitz teoremi, fonksiyonel analiz alanında önemli bir teoremdir. Bu teorem, Hilbert uzaylarında yer alan sınırlı operatörlerin spektral dağılımları hakkında bilgi sağlar. Hellinger-Toeplitz teoremi, Richard von Mises tarafından geliştirilmiş ve daha sonra Richard Courant ile Wilhelm Toeplitz tarafından genelleştirilmiştir.
Bu teoremin ana fikri, kompakt bir operatörün spektral dağılımının zorunlu olarak bir ölçüye yakınsamasıdır. Yani, bir Hilbert uzayında kompakt bir operatör düşünelim. Hellinger-Toeplitz teoremi, bu operatörün spektral dağılımının, herhangi bir yakınsak ölçüye limitte yakınsadığını ifade eder.
Hellinger-Toeplitz teoremi, matematiksel analizde çeşitli uygulamaları vardır. Özellikle kuantum mekaniği, iyi bilinen örneklerden biridir. Kompakt operatörlerin spektral teorisindeki bu teorem, kuantum mekaniği problemlerinin çözümünde kullanılır ve fiziksel sistemlerin spektral özelliklerini anlamak için önemli bir araçtır.
Hellinger-Toeplitz teoremi, fonksiyonel analizin derinliklerine inen bir teorem olup, matematiksel kanıtlama süreci oldukça karmaşıktır. Bu teoremi açıklamak ve anlamak için, spektral teorinin temel kavramlarına vakıf olmak gerekmektedir.
Hellinger-Toeplitz teoremi fonksiyonel analizin merkezi teoremlerinden biridir. Kompakt operatörlerin spektral dağılımlarının ölçüye yakınsamasını açıklar. Bu teorem, matematiksel analizde ve kuantum mekaniğinde önemli uygulamalara sahiptir. Matematik dünyasında büyük bir etkisi olan bu teorem, fonksiyonel analizin derinliklerine inmek isteyenler için ilgi çekici bir konudur.
Hellinger-Toeplitz Teoremi: Fonksiyonel Analizdeki Bilinmez Yıldız
Hellinger-Toeplitz teoremi, fonksiyonel analizin önemli bir kavramıdır. Bu teorem, bilinmeyen yıldız olarak da adlandırılır ve çeşitli matematiksel alanlarda büyük bir rol oynar. Bu makalede, Hellinger-Toeplitz teoreminin temellerini ve işlevlerini inceliyoruz.
Hellinger-Toeplitz teoremi, spektral teori ve operatör teorisi gibi konularla yakından ilişkilidir. Bu teorem, Hilbert uzayları üzerindeki sınırlı operatörlerin yoğunluklarını açıklar. Ayrıca, bu teorem matematiksel fizik ve istatistik gibi diğer alanlarda da uygulanabilir.
Teorem, adını iki ünlü matematikçi David Hilbert ve Otto Toeplitz’den almıştır. Hellinger-Toeplitz teoremi, bir operatörün orijinal fonksiyonu tamamen belirlemesi gerektiği durumlarda kullanılır. Bu teorem, bir operatörün olası tüm sınırlı uzantılarını bulmak için önemli bir araçtır.
Hellinger-Toeplitz teoremi, çeşitli matematiksel problemlere uygulanabilir. Özellikle, orijinal bir fonksiyonun bazı özellikleri hakkında bilgi sağlayarak, diferansiyel denklemlerin çözümlerini bulmada etkili olabilir. Ayrıca, Fourier analizi, dalgaleten analizi ve spektral teori gibi diğer matematiksel araçlarla birlikte kullanıldığında, daha geniş bir uygulama alanına sahiptir.
Hellinger-Toeplitz teoremi, matematiksel araştırma ve geliştirme açısından büyük bir ilgi çekmektedir. Bu teorem, fonksiyonel analizdeki derinlemesine çalışmalar ve karmaşık matematiksel yapılarla ilişkilendirilmiştir. Ayrıca, matematiksel teorilerin temelini anlamak için de önemlidir.
Hellinger-Toeplitz teoremi, fonksiyonel analizin önemli bir parçasıdır ve matematiksel araştırma ve geliştirmelerde büyük bir rol oynar. Bu teorem, operatörlerin yoğunlukları ve uzantıları hakkında bilgi sağlar. Matematiksel fizik, istatistik ve diğer alanlarda uygulanabilir. Hellinger-Toeplitz teoremi, fonksiyonel analizin bilinmez yıldızı olarak adlandırılır ve matematiksel araştırmalara yeni ufuklar açar.
Karmaşık Matematikte Gizemli Bir Teorem: Hellinger-Toeplitz
Giriş:
Matematik dünyasında, sayısız teorem ve keşiflerin yanı sıra bazen gerçekten gizemli ve etkileyici olanlar da vardır. Bu makalede, karmaşık matematikteki bir gizeme odaklanacağız: Hellinger-Toeplitz teoremi. Bu teorem, matematikçilerin kavramsal anlayışlarını derinleştiren ve sayısız uygulama alanına sahip olan bir matematiksel keşiftir.
Hellinger-Toeplitz Teoremi Nedir?
Hellinger-Toeplitz teoremi, fonksiyonel analiz alanında önemli bir yere sahiptir. Bu teorem, birer Hilbert uzayı olan H ve K’nın lineer operatörlerini içeren bir bağlantıyı ifade eder. Matematiksel ifadesi ise şu şekildedir: “Eğer H ve K, tamamen kesme özellikli Hilbert uzaylarıysa ve T, H’den K’ya bir sıkıştırma operatörüyse, o zaman T herhangi bir kesmeli operatörden daha çok bilgi sağlar.”
Bu teorem, genellikle istatistiksel veri analizi, görüntü işleme, doğrusal cebir ve matris teorisi gibi alanlarda uygulanır. Hellinger-Toeplitz teoremi, bu alanlardaki problemlerin çözümünde kullanılan matematiksel araçlar ve yöntemler üzerinde derinlemesine bir anlayış sunar.
Uygulamalar:
Hellinger-Toeplitz teoremi, istatistiksel veri analizi alanında özellikle büyük boyutlu veri kümelerinin sıkıştırılması, filtrelenmesi ve modellenmesi gibi problemlerin çözümünde yaygın olarak kullanılır. Ayrıca, görüntü işleme alanında da kullanılan bu teorem, görüntülerin sıkıştırılması, gürültüyü azaltma ve görüntü restorasyonu gibi uygulamalara da uyarlanabilir.
Matris teorisi ve doğrusal cebirde de Hellinger-Toeplitz teoreminin ardındaki derin kavramlar, matrisin yakınsaklık özellikleri, ters matris hesaplamaları ve spektral teori gibi konuları içerir. Bu bağlamda, teorem matris tabanlı algoritmaların tasarımında ve analizinde önemli bir rol oynar.
Sonuç:
Hellinger-Toeplitz teoremi, karmaşık matematik dünyasının gizemli bir köşesini temsil eder. Fonksiyonel analizdeki derinlikleri ve sayısız uygulama alanlarındaki etkisi, bu teoremin matematikçiler ve araştırmacılar için vazgeçilmez bir keşif haline gelmesini sağlamıştır. Hellinger-Toeplitz teoremini anlamak, matematiksel kavrayışı ve uygulamalardaki yaratıcılığı artırmak için önemli bir adımdır.
Fonksiyonel Analizin Şifreleri: Hellinger-Toeplitz Teoremi
Hellinger-Toeplitz teoremi, fonksiyonel analizin temel bir sonucudur ve bu alanda önemli bir rol oynar. Bu teorem, Hilbert uzaylarındaki sınırlı operatörlerin analizinde kullanılan bir araçtır. İşte Hellinger-Toeplitz teoremi hakkında detaylı bir açıklama.
Hellinger-Toeplitz teoremi, simetrik Toeplitz matrisleriyle ilgilidir. Bir Toeplitz matrisi, diyagonal elemanları aynı olan bir matristir. Örneğin, diyagonal elemanları c1, c2, c3 olan bir Toeplitz matrisi şu şekildedir:
c1 c2 c3
c2 c1 c2
c3 c2 c1
Hellinger-Toeplitz teoremi, bir fonksiyonun bir Hilbert uzayındaki simetrik Toeplitz matrisinin sınırlı bir operatöre yakınsadığını söyler. Yani, herhangi bir Hilbert uzayı elemanı olan bir fonksiyon, uygun bir şekilde seçilmiş bir simetrik Toeplitz matrisinin sınırlı bir operatörüne yaklaştırılabilir.
Bu teorem, pratik uygulamalarda büyük öneme sahiptir. Özellikle sinyal işleme ve veri analizi gibi alanlarda kullanılır. Hellinger-Toeplitz teoremi, çeşitli uygulamalarda veri sıkıştırma, filtreleme ve tahmin gibi işlemlerde kullanılan matematiksel araçlar sunar.
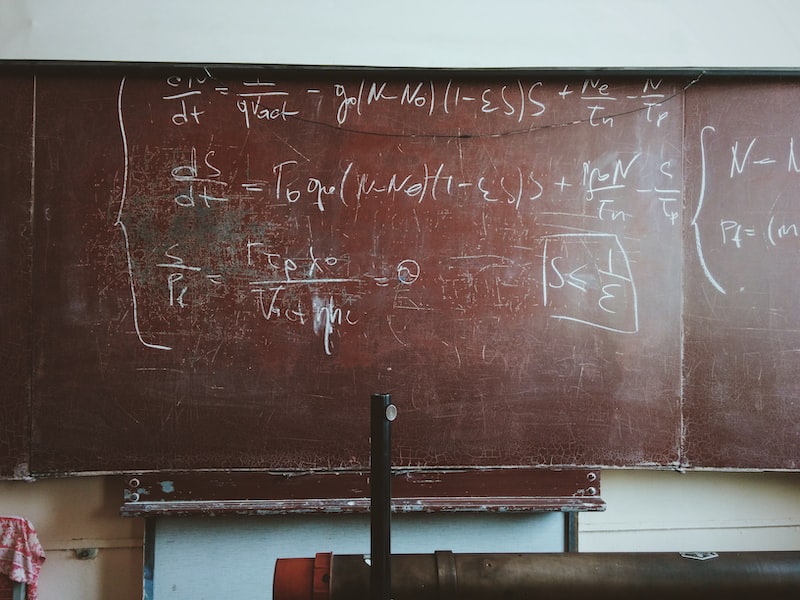
Hellinger-Toeplitz teoreminden yararlanarak, sinyallerin analizi ve sentezi gibi problemleri çözmek mümkündür. Bu teorem, özellikle zaman serileri ve görüntü işleme gibi alanlarda etkili bir şekilde kullanılır.
Hellinger-Toeplitz teoremi fonksiyonel analizin önemli bir sonucudur ve Hilbert uzaylarındaki sınırlı operatörlerin analizinde büyük bir rol oynar. Bu teorem, simetrik Toeplitz matrisleriyle ilgilidir ve pratik uygulamalarda sinyal işleme ve veri analizi gibi alanlarda yaygın olarak kullanılır. Hellinger-Toeplitz teoremi, fonksiyonların sınırlı operatörlere yakınsamasıyla ilgili önemli bir bağlantı sağlar ve matematiksel araştırmaların temelini oluşturur.
Hellinger-Toeplitz Teoremi: Matematik Dünyasının Sırrını Çözmek
Matematik dünyası, bilim ve mantıkla örülü bir evren olarak adlandırılabilir. Bu evrende, sayılar ve teoremler aracılığıyla sorunları çözerken bazen sıra dışı keşifler yapılır. Hellinger-Toeplitz Teoremi de tam olarak böyle bir keşiftir. Bu makalede, bu teorem hakkında daha fazla bilgi edinecek ve matematik dünyasının bu sırrını çözmeye bir adım atacağız.
Hellinger-Toeplitz Teoremi’nin temeli, matrislere dayanır. Matematikçiler David Hilbert ve Otto Toeplitz tarafından bağımsız olarak ortaya atılan bu teorem, büyük bir ilgi odağı haline gelmiştir. Teorem, simetrik pozitif belirli operatörler ve kompakt operatörlerle ilgilenir. İki farklı matematiksel alanın kesişiminde yer alan bu teorem, matrislerin sistemler ve denklemler ile olan ilişkisini inceler.
Bu teorem, istatistik, fizik, mühendislik ve ekonomi gibi çeşitli alanlarda uygulama bulmuştur. Özellikle veri analizi ve işaret işleme gibi disiplinlerde, Hellinger-Toeplitz Teoremi’nin sonuçları önemli bir role sahiptir. Teorem, matrislerin yerine göre nasıl davrandığını ve bu davranışın hangi sonuçları doğurduğunu gösterir. Bu sayede, karmaşık verileri daha anlaşılır hale getirmek ve daha kesin sonuçlara ulaşmak mümkün olur.
Hellinger-Toeplitz Teoremi’nin yüksek düzeyde özgüllüğü ve bağlamı, matematik camiasında büyük ilgi uyandırmıştır. Teorem, matrislerin yapısını analiz ederek birçok problemin çözülmesine katkı sağlar. Matematikçiler, bu teoremin ardındaki derinlikleri keşfetmek ve farklı alanlarda kullanımını genişletmek için çalışmalarını sürdürmektedir.
Hellinger-Toeplitz Teoremi matematik dünyasının önemli bir keşfidir. Bu teorem, matrislerin sistematik yapılarını inceleyerek karmaşık problemlerin çözülmesine yardımcı olur. İstatistikten mühendisliğe kadar birçok alanda uygulama bulan bu teorem, matematiksel düşüncenin gücünü ve evrenin gizemini ortaya koymaktadır. Hellinger-Toeplitz Teoremi’nin derinliklerinde kaybolmaya hazır mısınız?