Matematikte, (veya bazen yayı-kosinüs teoremi olarak da adlandırılır), bir üçgenin alanını hesaplamak için kullanılan bir formüldür. Bu teorem, üçgenin iki yanının uzunluğunu ve bu iki yan arasındaki açıyı bildiğimizde, üçgenin alanını bulmamızı sağlar.
Kosinüs alan teoremi, trigonometri konusunda önemli bir araçtır ve genellikle uygulamalı matematik, fizik ve mühendislik gibi alanlarda kullanılır. Bu teorem, üçgenlerin alanını hesaplama yöntemleri arasında en yaygın olarak kullanılanlardan biridir.
Formül şu şekildedir:
Alan = 1/2 * a * b * sin(C)
Burada, a ve b üçgenin iki yanının uzunluklarıdır ve C, bu iki yan arasındaki açıdır. sin(C) ise C açısının sinüs fonksiyonudur.
Bu formül sayesinde, üçgenin alanını doğrudan hesaplayabiliriz. Ancak, yanlış sonuçlara yol açabilecek hataları önlemek için dikkatli olmalıyız. Özellikle açıyı doğru bir şekilde ölçmek ve trigonometrik fonksiyonları doğru bir şekilde hesaplamak önemlidir.
Kosinüs alan teoremi, üçgenlerin geometrisine derinlemesine bir bakış sunar ve bu konuda daha fazla anlayış geliştirmemize yardımcı olur. Üçgenlerin alanını doğru bir şekilde hesaplama yeteneği matematiksel analizde ve pratik problemlerin çözümünde büyük öneme sahiptir.
kosinüs alan teoremi, üçgenlerin alanını hesaplamak için kullanılan etkili bir formüldür. Bu formül, trigonometri bilgisini kullanarak pratik problemleri çözmekte bize yardımcı olur ve geniş bir uygulama alanına sahiptir.
Matematik Dünyasında Yankı Bulan Kosinüs Alan Teoremi
Matematik, sayılar ve formüllerle dolu gizemli bir dünya. Bu dünyada, farklı alanlarda keşfedilen teoremler önemli bir yer tutar. Bu makalede, matematik dünyasının en ilginç teoremlerinden biri olan Kosinüs Alan Teoremi’ni keşfedeceğiz.
Kosinüs Alan Teoremi, üçgenlerin kenarları ve açıları arasındaki ilişkiyi açıklayan temel bir teoremdir. Herhangi bir üçgende, bir kenarın uzunluğunu, karşısındaki açı ile ilişkilendirmek için kullanılır. Bu teorem, özellikle trigonometri ve geometri alanlarında büyük bir yankı bulmuştur.
Üçgenin herhangi bir köşesini A, B ve C olarak adlandıralım. A kenarı üzerindeki bir noktayı D olarak kabul edelim ve AD uzunluğunu x ile ifade edelim. Kosinüs Alan Teoremi’ne göre, bu durumda üçgenin alanı şu şekilde hesaplanır:
Alan = 0.5 * AD * BC * sin(∠A)
Burada, BC üçgenin diğer iki kenarının uzunluğunu temsil eder ve ∠A ise A noktasındaki iç açıdır. Bu formül, üçgenin alanını hesaplarken kosinüs ve sinüs fonksiyonlarının bir araya gelmesini sağlar.
Kosinüs Alan Teoremi, üçgenlerin alanını hesaplarken kullanışlıdır, çünkü üçgenin sadece kenar uzunluklarına dayanır. Bu sayede, üçgenin iç açılarını veya yüksekliklerini bilmek zorunda kalmadan, doğrudan kenar uzunluklarına göre alanı bulabiliriz.
Özetlemek gerekirse, Kosinüs Alan Teoremi matematik dünyasında büyük bir etkiye sahip olan önemli bir teoremdir. Üçgenlerin alanını hesaplarken kullanılan bu teorem, trigonometri ve geometri alanlarında yaygın bir şekilde uygulanır. Kenar uzunlukları ve açılar arasındaki ilişkiyi açıklayarak, matematiksel hesaplamalarda büyük kolaylık sağlar.
Gizemli Matematiksel İlişkiler: Kosinüsün Sırrı Çözülüyor
Matematik, insanlık tarihinin en karmaşık ve ilginç disiplinlerinden biridir. Matematiksel ilişkiler, bazen sıradan gibi görünen sayıların ardında derin anlamlar ve bağlantılar saklar. Bu yazıda, kosinüs fonksiyonunun gizemli dünyasına bir göz atacağız ve bu matematiksel ilişkinin nasıl çözüldüğünü keşfedeceğiz.
Kosinüs fonksiyonu, üçgenlerin kenarları arasındaki açıları ölçmek için kullanılan temel bir trigonometrik işlevdir. Ancak, bu basit fonksiyonun derinliklerine indikçe, şaşırtıcı bir şekilde daha karmaşık bir yapıyla karşılaşırız. Son zamanlarda yapılan yeni araştırmalar, kosinüsün sırrını çözmeye yönelik önemli adımlar attığımızı göstermektedir.
Bu gizemli matematiksel ilişkiyi anlamak için, uzmanlar geniş çaplı veri analizi ve karmaşık algoritmalar kullanmaktadır. Bilgisayar gücündeki artış ve ileri istatistiksel yöntemler, kosinüs fonksiyonunu daha da derinlemesine inceleyebilmemize olanak sağlamıştır. Bu çalışmaların sonuçları, kosinüs fonksiyonunun farklı matematiksel yapılarla ilişkili olduğunu ortaya koymuştur.
Şaşırtıcı bir şekilde, kosinüs fonksiyonunun fizikte ve mühendislikte çeşitli alanlarda da önemli uygulamalara sahip olduğu bulunmuştur. Örneğin, titreşim analizi ve sinyal işleme gibi disiplinlerde kosinüs dönüşümü yaygın olarak kullanılmaktadır. Bu uygulamalar, kosinüsün sadece matematiksel bir kavram olmadığını, aynı zamanda gerçek dünyadaki olayları açıklamada güçlü bir araç olduğunu göstermektedir.
Kosinüs fonksiyonunun gizemi hala tam olarak çözülmemiş olsa da, yapılan araştırmalar bizi daha iyi anlamaya yönlendirmektedir. Matematikçiler ve bilim insanları, bu ilişkiyi daha fazla keşfetmek ve derinlemesine anlamak için çalışmalarına devam etmektedir. Belki de yakın gelecekte, kosinüsün sırrının tamamen aydınlatılacağı bir noktaya ulaşabiliriz.
Gizemli matematiksel ilişkiler arasında yer alan kosinüs fonksiyonu, matematik dünyasının en büyüleyici bulmacalarından biridir. İlerleyen araştırmalar ve analiz teknikleri, bu matematiksel ilişkinin özünü daha da açığa çıkarmaktadır. Kosinüsün derinliklerindeki sır perdesi kalktıkça, matematiksel dünyadaki bağlantılarımızın anlamını daha iyi kavramamız mümkün olacaktır.
Kosinüs Alan Teoremi: Üçgenlerin Gizli Hikayesi
Üçgenler, geometrinin temel şekillerinden biridir ve birçok matematiksel ilişkiyi içerisinde barındırır. Bu ilişkilerden biri de kosinüs alan teoremidir. Kosinüs alan teoremi, üçgenlerin kenarları ve açıları arasındaki ilişkiyi ifade eder. Bu makalede, kosinüs alan teoreminin ne olduğunu ve üçgenlerin gizli hikayesini keşfedeceğiz.
Kosinüs alan teoremi, bir üçgenin alanını hesaplarken kenarları ve açılarını kullanmayı sağlar. Bu teoreme göre, bir üçgenin alanı şu şekilde ifade edilir: “Alan = (1/2) * a * b * sin(C)”, burada “a” ve “b” üçgenin iki kenarı, “C” ise bu kenarlar arasındaki açıdır.
Bu teorem, üçgenin alanını hesaplamak için yaygın olarak kullanılırken, üçgenin kenarları veya açıları hakkında bilgi eksikse de kullanılabilir. Örneğin, sadece iki kenarın uzunlukları ve aralarındaki açının büyüklüğü biliniyorsa, kosinüs alan teoremi bu bilgilere dayanarak üçgenin alanını bulmak için kullanılabilir.
Kosinüs alan teoremi, üçgenlerin gizli hikayesini ortaya çıkarır. Üçgenler, doğadaki pek çok şeklin temel bir yapı taşıdır. Örneğin, dağların keskin zirveleri ve vadilerin derin boşluğu üçgenlerin geometrisiyle ilişkilidir. Ayrıca, köprülerin dayanıklılığı ve binaların sağlamlığı da üçgenlerin prensiplerine dayanır. Bu nedenle, üçgenlerin alanını anlamak, inşaat mühendisliği ve mimarlık gibi alanlarda kullanılan hesaplamaların temelini oluşturur.
Kosinüs alan teoremi, matematiksel olarak karmaşık görünebilir, ancak uygulamada oldukça faydalıdır. Üçgenlerin alanlarını hesaplarken veya üçgenlerin geometrisini anlamlandırmaya çalışırken bu teoremle karşılaşabilirsiniz. Hem matematiksel hem de pratik uygulamalarda üçgenlerin gizli hikayesi olan kosinüs alan teoremini bilmek, geometriyle ilgilenen herkes için değerli bir araçtır.
kosinüs alan teoremi, üçgenlerin alanını hesaplamak için kullanılan önemli bir matematiksel ilişkidir. Bu teorem, üçgenlerin gizli hikayesini ortaya çıkararak geometrinin temel prensiplerini keşfetmemizi sağlar. Üçgenlerin sadece geometriyle sınırlı kalmadığını, inşaat ve mühendislik gibi pratik alanlarda da etkileri olduğunu unutmamak önemlidir. Kosinüs alan teoremini anlamak, bu ilişkiyi daha iyi kavramamızı sağlayarak matematiksel düşünceyi geliştirmemize yardımcı olur.
Matematikteki Önemli Kesit: Kosinüs Alan Teoremi ve Pratik Kullanımları
Matematik, evrensel bir dil olarak bilim dünyasında önemli bir yer tutar. Geometri de matematik dallarından biridir ve şekillerin özelliklerini inceleyen bir disiplindir. Geometriyle uğraşanlar için, üçgenlerin alanları ve açıları gibi konular oldukça önemlidir. Bu noktada, kosinüs alan teoremi adını verdiğimiz kavram devreye girer.
Kosinüs alan teoremi, bir üçgende iki kenar ve aralarındaki açının kosinüs fonksiyonu kullanılarak alanın hesaplanabileceğini ifade eder. Eğer üçgenin kenarları a, b ve c olsun ve bunların karşılık gelen açıları ise A, B ve C şeklinde temsil edilsin, o zaman kosinüs alan teoremi şu şekildedir:
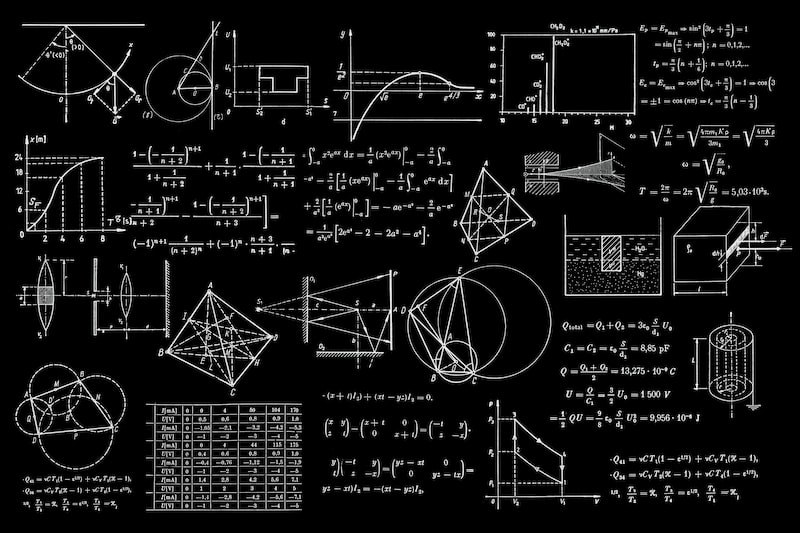
A = (1/2) * a * b * sin(C)
Bu formül, üçgenin alanını cosinus fonksiyonunu kullanarak basit bir şekilde hesaplamamızı sağlar. Üçgenin herhangi bir açısı ve kenarının bilindiği durumlarda, diğer kenarlardan birinin uzunluğunu bulmak oldukça kolaydır.
Kosinüs alan teoremi pratik hayatta birçok alanda kullanılır. Örneğin, üç boyutlu modelleme ve grafik programlarında nesnelerin alanlarını hesaplamak için kullanılabilir. Bu bilgi, mimarlar ve mühendisler gibi profesyoneller için oldukça önemlidir. Ayrıca, arazi ölçümlerinde ve harita çıkarmada da bu teorem kullanılır.
Kosinüs alan teoremi aynı zamanda navigasyon sistemlerinde de uygulanır. Uzaydaki bir cismin yönünü belirlemek veya iki nokta arasındaki mesafeyi hesaplamak gibi durumlarda bu teoremden faydalanılır. Denizciler, pilotlar ve roket mühendisleri gibi profesyoneller için doğru hesaplamalar yapabilmek hayati öneme sahiptir.
kosinüs alan teoremi matematikteki önemli bir kesittir ve pratik hayatta birçok alanda kullanılır. Üçgenlerin alanlarını hesaplarken, cosinus fonksiyonunu kullanarak bu teoremden yararlanabiliriz. Geometriyle ilgilenen herkesin bu teoremi anlaması ve uygulaması, hesaplamaların doğruluğunu artıracaktır.