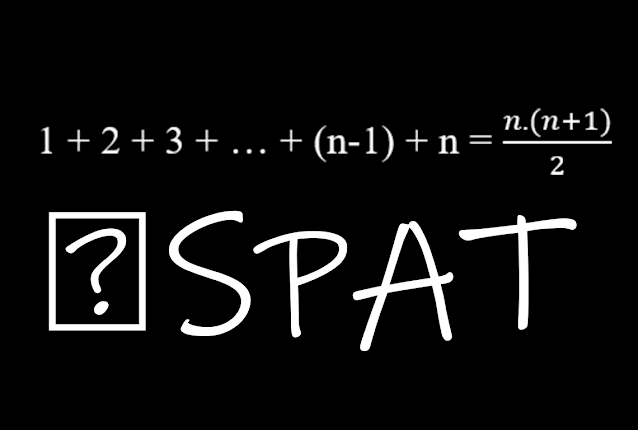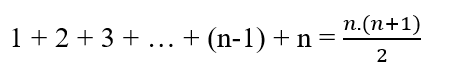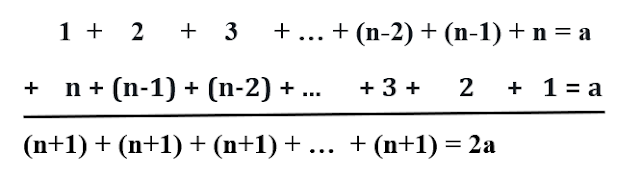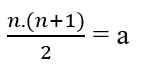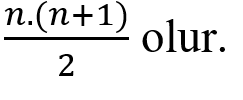Terimler toplamı formülü ispatı gauss – terimler toplamı formülü ispatı gauss
Bu yazımızda daha önce MATEMATİKTE KULLANILAN İSPAT YÖNTEMLERİ başlıklı yazımızda tümevarım yöntemiyle ispatladığımız terimler toplamı formülünün iki farklı ispatını daha yapacağız. Ama önce bu teoremin bulunuş hikayesine bir göz atalım.
Gauss ‘un ilkokul öğretmeni sınıftan çıkmak istemiş. Çocuklara boş durmasınlar oyalansınlar diye işlem kalabalığı olan ” zor ” bir soru sormuş.
“1 ‘den 100 ‘e kadar olan sayıların toplamı kaçtır?” Bu soruyu sorduktan sonra daha sınıftan çıkamadan kapının eşiğinde Gauss oturduğu yerden 5050 diye bağırmış. Gauss ‘un ilkokul öğretmeni donakalmış. Hesap yeteneği ne kadar iyi de olsa bu kadar hızlı bir şekilde nasıl hesapladı? İşte küçük Gauss ‘un o formülü:
Şimdi de bu teoremi cebirsel ve geometrik olacak şekilde 2 farklı yöntemle daha ispatlayalım.
TERİMLER TOPLAMI FORMÜLÜNÜN İSPATI – 1.yol
1 ‘den n ‘e kadar olan sayıları toplayalım ve bu toplamın sonucuna a diyelim. Aynı şekilde tam altına n ‘den 1 ‘e kadar olan sayıları toplayalım ve bu toplama a diyelim.
1 + 2 + 3 + … + (n-2) + (n-1) + n = a
n + (n-1) + (n-2) + … + 3 + 2 + 1 = a
şimdi bu iki eşitliği birbiri ile toplayalım.
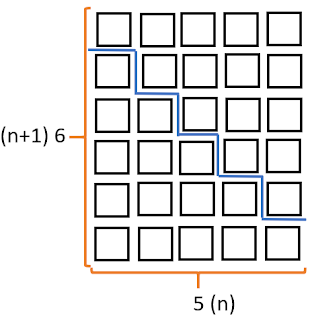
Elimize n tane (n+1) geçti. n . (n+1) çarpımı ise 2a ‘ya eşit oldu.
n . (n+1) = 2.a
2 ‘yi karşı tarafa attığımızda:
Şimdi ise 2. yola bakalım.
TERİMLER TOPLAMI FORMÜLÜNÜN İSPATI – 2.yol
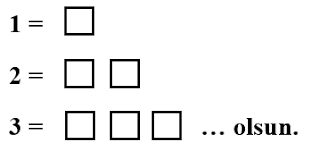
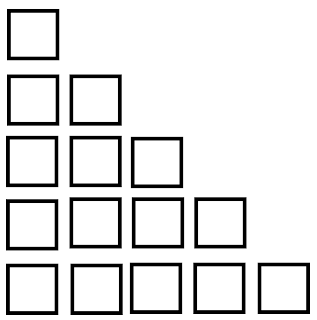
Her sayıyı kare olarak gösterelim. Örneğin: