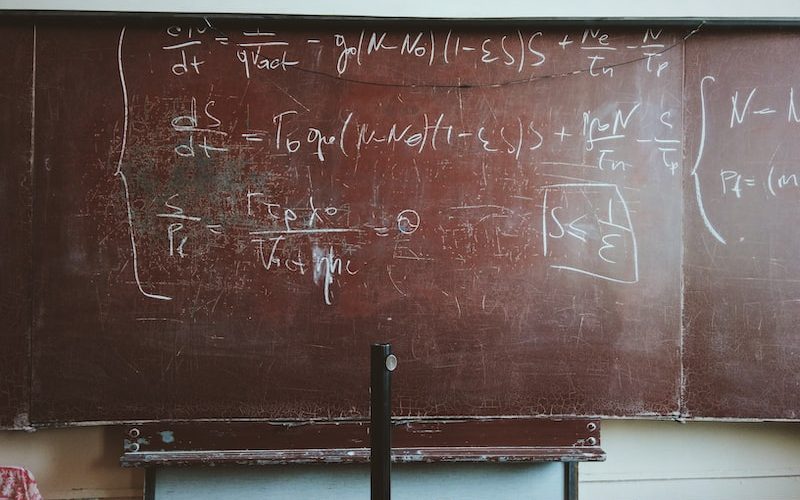Tüylü Top Teoremi, cebirsel topoloji alanında önemli bir konudur. Bu teorem, topolojik uzayların homotopi teorisi ile ilgilenir ve teoriye derin bir anlayış sunar. Tüylü Top Teoremi, topolojik uzayların tam olarak nasıl sınıflandırılabileceğini ortaya koyar ve bu da matematikçilerin topolojinin temel sorularını çözmelerine yardımcı olur.
Bu teoremin en ilginç tarafı, tüylü topolojik uzayların homotopik özelliklerinin, bu uzayların toplamdaki lineer uzayların homotopik özellikleriyle bağlantılı olduğunu göstermesidir. Yani, tüylü topolojik uzayların şekilleri ve özellikleri, içerdikleri vektör uzaylarının şekil ve özellikleriyle yakından ilişkilidir.
Bunun yanı sıra, Tüylü Top Teoremi, topoloji ve cebir arasındaki bağı güçlendiren önemli bir araştırma alanıdır. Cebirsel topoloji, soyut cebir ve topolojinin kesişiminde yer alan bir disiplindir ve Tüylü Top Teoremi, bu iki alanın birlikte nasıl çalışabileceğini gösteren bir örnektir.
Tüylü Top Teoremi’nin uygulamaları da oldukça geniştir. Özellikle fizik ve mühendislik gibi disiplinlerde, topolojik uzayların tüylü yapılarının incelenmesi, karmaşık sistemlerin davranışını anlamak için önemli bir araçtır. Bu teorem, veri analitiği ve makine öğrenme gibi alanlarda da kullanılabilecek güçlü matematiksel yöntemler sunar.
Tüylü Top Teoremi cebirsel topolojinin temel taşlarından biridir. Bu teorem, topolojik uzayların homotopik özelliklerini anlamamızda, soyut cebir ve topoloji arasındaki ilişkinin güçlenmesinde ve farklı disiplinlerde uygulamalarının bulunmasında önemli bir role sahiptir. Tüylü Top Teoremi’nin araştırmacılar ve matematikçiler için heyecan verici bir konu olduğunu söyleyebiliriz.
Cebirsel Topoloji: Tüylü Top Teoremi’nin Gizemi
Cebirsel topoloji, matematikte önemli bir araştırma alanıdır ve tüylü top teoremi bu alanda büyük bir gizem olarak karşımıza çıkar. Bu makalede, cebirsel topolojinin temel kavramlarına değinecek ve tüylü top teoreminin nasıl bir gizem olduğunu açıklayacağız.
Cebirsel topolojide, topoloji ve cebir arasındaki ilişki incelenir. Topoloji, noktaların yakınlığını ve sürekliliği tanımlayan bir matematik dalıdır. Cebir ise matematiksel yapıları ve işlemleri inceleyen bir disiplindir. Cebirsel topoloji, bu iki alanın birbirini tamamladığı bir araştırma sahasıdır.
Tüylü top teoremi, cebirsel topolojinin en ilginç unsurlarından biridir. Bu teorem, bir topolojik uzayın, yani bir kümenin üzerinde belirli bir yapıya sahip olan noktaların topluluğunun, belli koşulları sağladığı durumda, her zaman bir tüylü yapıya sahip olacağını ifade eder. Bu yapı, topolojik uzayın bazı özelliklerini aydınlatır ve ilginç sonuçlara yol açar.
Tüylü top teoremi, matematikçiler arasında uzun süredir merak uyandıran bir gizemdir. Bu teoremin kanıtlanması zorluğu ve sonucunda elde edilen sonuçların derinliği, onu matematik dünyasında heyecan verici kılar. Matematikçiler, tüylü top teoremini anlamak için çeşitli yaklaşımlar geliştirmişlerdir ve hala daha bu konuda araştırmalar yapılmaktadır.
Tüylü top teoremi, matematiksel düşünceye yeni perspektifler sunar ve farklı alanlarda uygulamaları vardır. Özellikle diferansiyel denklemler, fizik, istatistik ve ekonomi gibi disiplinlerde kullanılabilir. Bu teorem, matematiksel düşüncenin sınırlarını zorlayarak, yeni keşiflerin yolunu açar.
cebirsel topoloji, matematik dünyasının önemli bir alanıdır ve tüylü top teoremi de bu alandaki en büyüleyici gizemlerden biridir. Bu makalede, cebirsel topolojinin temellerini anlattık ve tüylü top teoreminin ne kadar merak uyandıran bir konu olduğunu vurguladık. Matematikçilerin bu teoremi çözme çabaları, matematiksel düşüncenin sınırlarını zorlamanın ve yeni keşiflerin peşinde olmanın bir göstergesidir.
Matematik Dünyasında Çığır Açan Tüylü Top Teoremi
Matematik, her geçen gün kendini yenileyen bir bilim dalıdır. Bu sürekli değişen ve gelişen alanda çığır açan teoremlerden biri de “Tüylü Top Teoremi”dir. Bu teorem, matematiksel düşünceyi farklı bir boyuta taşıyarak akademik çevrelerde büyük heyecan yaratmıştır.
Tüylü Top Teoremi, topoloji ve geometri alanlarını bir araya getirerek kusursuz bir denge yakalamıştır. Bu teoreme göre, tek bir tüy üzerinde duran bir topun, belirli koşullar altında hareket etmesiyle oluşan izleyenin matematiksel modellemesi yapılmıştır. Bu modelleme, topun hareketinin basit bir eğriye değil, karmaşık ve ilginç bir şekilde gerçekleştiğini ortaya koyar.
Bu teoremin büyük önemi, matematiksel dünyadaki problemlerin çözümünde yol gösterici olmasıdır. Özellikle fizik, mühendislik ve robotik gibi disiplinlerde, Tüylü Top Teoremi’nin uygulanabilmesi sayesinde daha doğru sonuçlar elde edilmektedir. Bununla birlikte, bu teorem sayesinde matematiksel çıkarımların sınırlarını zorlamak mümkün olmuş ve yeni keşiflere kapı aralanmıştır.
Tüylü Top Teoremi’nin ilginçliği, sadece matematikçileri değil aynı zamanda genel halkı da etkilemektedir. Teorem, karmaşık matematiksel kavramları anlaşılır bir şekilde sunarak, matematiği herkesin anlayabileceği bir dilde ifade eder. Matematikle ilgilenenler için heyecan verici bir konudur çünkü bu teorem, matematiğin soyut dünyasını somut bir deneyim haline getirir.
Tüylü Top Teoremi, matematik dünyasında büyük bir çığır açmıştır. Bu teorem, topoloji ve geometriyi birleştirerek farklı bir perspektif sunar ve matematiksel problemlerin çözümünde yol gösterici olur. Aynı zamanda, insanların matematiği daha anlaşılır ve ilgi çekici bulmasına yardımcı olur. Tüylü Top Teoremi’nin keşfi, matematiksel düşüncenin sınırlarını zorlamaya devam edeceğimiz bir geleceğe işaret etmektedir.
Tüylü Top Teoremi: Karmaşık Matematiksel İlişkilerin Sırrı
Matematik, evrenin derinliklerindeki bilgeliği keşfetmemize yardımcı olan büyülü bir dildir. Karmaşık matematiksel ilişkiler ve denklemler, bazen anlaşılması zor gibi görünse de, gerçek dünyadaki birçok fenomeni açıklamak için hayati öneme sahiptir. Bu bağlamda, matematikçilerin üzerinde çalıştığı tüylü top teoremi, bu karmaşıklığı aydınlatmada ilginç bir yol sunuyor.
Tüylü top teoremi, matematiksel analizdeki diferansiyel geometri disiplinine ait önemli bir kavramdır. Bir topun yüzeyine yerleştirilen tüylerin nasıl hareket ettiğini tanımlayan bu teorem, topun içindeki eğriliği ve dönüşleri açıklar. Başka bir deyişle, bu teorem, topun şekline göre tüylerin hareket etme şeklini betimler ve matematiksel olarak ifade eder.
Bu teoremin ilginç yanı, topun içindeki tüylerin belirli bir doku veya kalıpla etkileşime girmediği durumlarda bile, her noktanın farklı bir yönde tüylerin hareket ettiğidir. Bu, matematiksel bir modelin, çok sayıda bağımsız ve karmaşık değişkenin birleşimiyle gerçek dünyadaki olayları nasıl doğru bir şekilde temsil edebildiğini gösteren önemli bir örnektir.
Tüylü top teoremi, matematiksel analizdeki integrasyon, diferansiyel denklemler ve çok değişkenli fonksiyonlar gibi alanlarda da büyük bir rol oynamaktadır. Özellikle fizik, mühendislik ve bilgisayar bilimlerinde kullanılan karmaşık modellerin çözümünde önemli bir araçtır. Bu teorem, karmaşık matematiksel ilişkilerin özünü yakalamamıza yardımcı olur ve bu sayede gerçek dünyadaki problemleri daha iyi anlamamıza ve çözmemize olanak sağlar.
tüylü top teoremi, matematiksel düşüncenin gücünü ve etkisini gösteren bir örnektir. Karmaşık matematiksel ilişkileri aydınlatarak, gerçek dünyayı daha iyi anlamamıza ve keşfetmemize yardımcı olur. Matematikçilerin çalışmalarında bu teoremi kullanarak, evrenin derinliklerindeki sırların izini sürmeye devam ediyoruz.
Tüylü Topların Gizemli Dansı: Cebirsel Topolojinin Yeni Keşfi
Cebirsel topoloji, matematik dünyasında heyecan verici bir araştırma alanıdır. Bu disiplin, karmaşık yapıları ve şekilleri inceleyerek soyut kavramları çözümlemeyi amaçlar. Son yıllarda, tüylü toplar adı verilen ilginç bir nesne, cebirsel topoloji alanında büyük bir keşif olarak ortaya çıktı.
Tüylü toplar, birden çok boyutta sarkan tel demetlerini temsil eder. Bu demetler, mantıksal ilişkileri ve geometrik özellikleriyle ilgili bilgilere sahiptir. Cebirsel topologlar için bu tüylü topların dansı, yeni bir anlam ve anlayış sağlamaktadır.
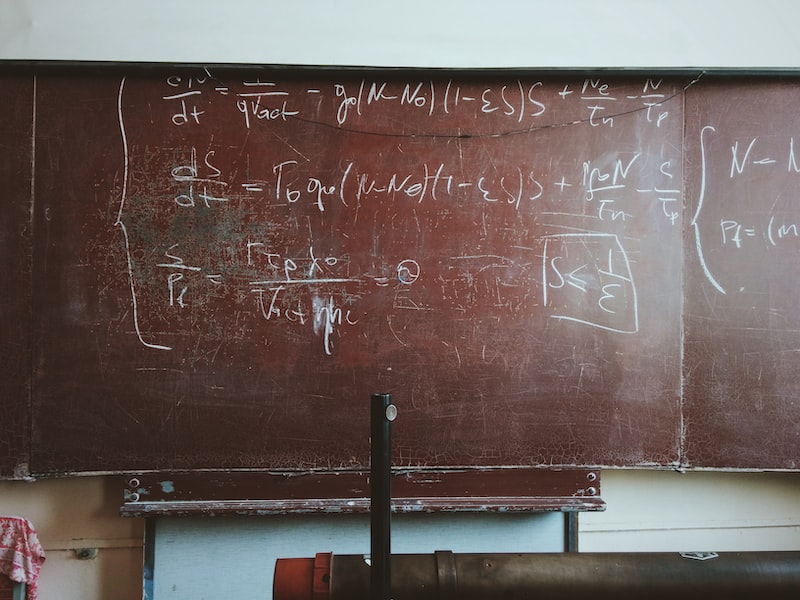
Bu keşif, cebirsel topolojideki bazı temel sorunlara ışık tutmuştur. Birçok matematiksel problemi çözebilmek için tüylü topların bağlantıları ve dönüşüm özellikleri incelenmektedir. Örneğin, topolojik düğümleri analiz ederek, karmaşık ağların yapısını daha iyi anlamak mümkün olabilir.
Tüylü topların gizemli dansı, onları son derece ilgi çekici hale getirmektedir. Bu dans, şekil değiştirme ve dönüşüm yetenekleriyle birlikte gerçekleşir. Matematikçiler, bu hareketleri analiz ederek topolojik özellikleri daha iyi anlamak için çabalıyor.
Cebirsel topolojinin bu yeni keşfi, matematik dünyasında büyük heyecan yaratmıştır. Bu alandaki araştırmalar, veri analitiği, yapay zeka ve mühendislik gibi farklı alanlarda da uygulamaları olan önemli sonuçlar doğurabilir. Tüylü topların dansı, karmaşık sistemlerin anlaşılmasına ve bu sistemlerin günlük yaşamımızdaki etkilerini değerlendirmeye yardımcı olabilir.
cebirsel topolojinin yeni keşfi olan tüylü topların gizemli dansı, matematik dünyasında büyük bir ilgi uyandırmaktadır. Bu alandaki araştırmalar, bilim insanlarının soyut kavramları ve karmaşık yapıları daha iyi anlamalarını sağlamaktadır. Tüylü topların şekil değiştirme ve dönüşüm yetenekleri, bilimsel ve teknolojik ilerlemelerde yeni kapılar açabilir ve gelecekteki çalışmalara ilham verebilir.