Uzayda iki nokta arası uzaklık formülünün ispatı için sadece Pisagor Teoremi’ni bilmemiz yeterlidir. Bu ispat düzlemdeki noktalar arası uzaklık formülünün ispatından çok da farklı değildir.
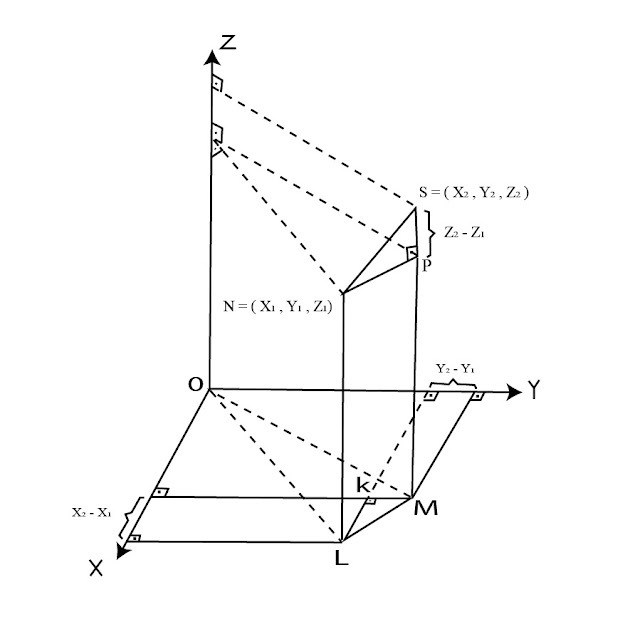
Uzayda dik koordinatlarla verilen N = (X1, Y1, Z1) ve S = (X2, Y2, Z2) noktaları arasındaki uzaklığı bulmak için kullandığımız formül
olur.
UZAYDA İKİ NOKTA ARASI UZAKLIK FORMÜLÜNÜN İSPATI
Bu formülü ispatlamak için düzlemde iki nokta arası uzaklığı bulmak için kullandığımız formülün ispatında olduğu gibi N = (X1, Y1, Z1) ve S = (X2, Y2, Z2) noktalarını kullanarak bir dik üçgen oluşturalım.
Bu dik üçgenin tabanının uzunluğu ile aynı uzunlukta bir dik üçgeni xy düzlemine çizelim. Bu kısımda yapmamız gereken uzunlukları aynı olan kenarlar yardımı ile formülü ispatlamaktır.
İlk olarak Pisagor teoremini kullanarak düzlemde bulunan LMK üçgeninin bir kenarı olan LM (aynı zamanda NP) kenarının uzunluğunu bulalım.
olur.
Şimdi elde ettiğimiz bu eşitliği uzayda bulunan NSP üçgenine Pisagor Teoremi uygulayarak kullanalım.
Uzayda bulunan NSP üçgenine Pisagor Teoremi’ni uygularsak
elde ederiz.
Uzayda ve düzlemde bulunan üçgenlere Pisagor Teoremi uygulayarak bulduğumuz eşitliklerde ortak olan kenar | NP | ve uzunluğu bilinen | PS | kenarları son eşitlikte yerine yazılırsa
| NP |2 = (X2 – X1)2 + (Y2 – Y1)2
| PS |2 = (Z2– Z1)2
elde edilir. Böylece uzayda bulunan iki nokta arasındaki uzaklığı veren formül sadece Pisagor Teoremi ile ispatlanmış olur. Bu teoremin ispatında çokça bahsettiğimiz Pisagor teoreminin ispatına buraya tıklayarak ulaşabilirsiniz.
Yorumlarınız bizim için çok değerli. Lütfen yorum yapmayı unutmayın. Daha fazla içerik için Anasayfa’ya gidebilir yada İletişim bölümünden benim ile iletişime geçebilirsiniz.